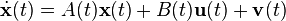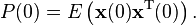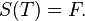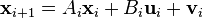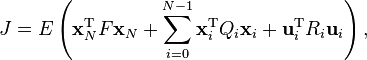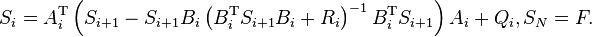Linear-quadratic-Gaussian control

From Wikipedia, the free encyclopedia

In control theory, the linear-quadratic-Gaussian (LQG) control problem is one of the most fundamental optimal control problems. It concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information (i.e. not all the state variables are measured and available for feedback) and undergoing control subject to quadratic costs. Moreover the solution is unique and constitutes a linear dynamic feedback control law that is easily computed and implemented. Finally the LQG controller is also fundamental to the optimal control of perturbed non-linear systems.[1]

The LQG controller is simply the combination of a Kalman filter i.e. a linear-quadratic estimator (LQE) with a linear-quadratic regulator (LQR). The separation principle guarantees that these can be designed and computed independently. LQG control applies to both linear time-invariant systems as well as linear time-varying systems. The application to linear time-invariant systems is well known. The application to linear time-varying systems enables the design of linear feedback controllers for non-linear uncertain systems.

The LQG controller itself is a dynamic system like the system it controls. Both systems have the same state dimension. Therefore implementing the LQG controller may be problematic if the dimension of the system state is large. The reduced-order LQG problem (fixed-order LQG problem) overcomes this by fixing a-priori the number of states of the LQG controller. This problem is more difficult to solve because it is no longer separable. Also the solution is no longer unique. Despite these facts numerical algorithms are available[2][3][4][5] to solve the associated optimal projection equations[6][7] which constitute necessary and sufficient conditions for a locally optimal reduced-order LQG controller.[2]

Finally, a word of caution. LQG optimality does not automatically ensure good robustness properties.[8] The robust stability of the closed loop system must be checked separately after the LQG controller has been designed. To promote robustness some of the system parameters may be assumed stochastic instead of deterministic. The associated more difficult control problem leads to a similar optimal controller of which only the controller parameters are different.[3]

Mathematical description of the problem and solution

Continuous time

Consider the linear dynamic system,

{\dot {{\mathbf {x}}}}(t)=A(t){\mathbf {x}}(t)+B(t){\mathbf {u}}(t)+{\mathbf {v}}(t)
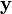{\mathbf {y}}(t)=C(t){\mathbf {x}}(t)+{\mathbf {w}}(t),

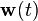where {{\mathbf {x}}} represents the vector of state variables of the system, {{\mathbf {u}}} the vector of control inputs and {{\mathbf {y}}} the vector of measured outputs available for feedback. Both additive white Gaussian system noise {\mathbf {v}}(t) and additive white Gaussian measurement noise {\mathbf {w}}(t) affect the system. Given this system the objective is to find the control input history {{\mathbf {u}}}(t) which at every time 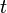{{\mathbf {}}}t may depend only on the past measurements {{\mathbf {y}}}(t'),0\leq t'<t such that the following cost function is minimized,

J=E\left({{\mathbf {x}}^{{\mathrm T}}}(T)F{{\mathbf {x}}}(T)+\int _{{0}}^{{T}}{{\mathbf {x}}^{{\mathrm T}}}(t)Q(t){{\mathbf {x}}}(t)+{{\mathbf {u}}^{{\mathrm T}}}(t)R(t){{\mathbf {u}}}(t)\,dt\right),
F\geq 0,\quad Q(t)\geq 0,\quad R(t)>0,

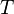where {{\mathbf {}}}E denotes the expected value. The final time (horizon) {{\mathbf {}}}T may be either finite or infinite. If the horizon tends to infinity the first term 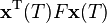{{\mathbf {x}}}^{{\mathrm T}}(T)F{{\mathbf {x}}}(T) of the cost function becomes negligible and irrelevant to the problem. Also to keep the costs finite the cost function has to be taken to be {{\mathbf {}}}J/T.

The LQG controller that solves the LQG control problem is specified by the following equations,

{\dot {{\hat {{\mathbf {x}}}}}}(t)=A(t){\hat {{\mathbf {x}}}}(t)+B(t){{\mathbf {u}}}(t)+K(t)\left({{\mathbf {y}}}(t)-C(t){\hat {{\mathbf {x}}}}(t)\right),{\hat {{\mathbf {x}}}}(0)=E\left({{\mathbf {x}}}(0)\right)
{{\mathbf {u}}}(t)=-L(t){\hat {{\mathbf {x}}}}(t).

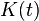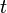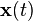The matrix {{\mathbf {}}}K(t) is called the Kalman gain of the associated Kalman filter represented by the first equation. At each time {{\mathbf {}}}t this filter generates estimates {\hat {{\mathbf {x}}}}(t) of the state {{\mathbf {x}}}(t) using the past measurements and inputs. 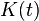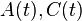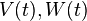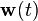The Kalman gain {{\mathbf {}}}K(t) is computed from the matrices {{\mathbf {}}}A(t),C(t), the two intensity matrices {\mathbf {}}V(t),W(t) associated to the white Gaussian noises {\mathbf {v}}(t) and {\mathbf {w}}(t) and finally E\left({{\mathbf {x}}}(0){{\mathbf {x}}}^{{\mathrm T}}(0)\right). These five matrices determine the Kalman gain through the following associated matrix Riccati differential equation,

{\dot {P}}(t)=A(t)P(t)+P(t)A^{{\mathrm T}}(t)-P(t)C^{{\mathrm T}}(t){{\mathbf {}}}W^{{-1}}(t)C(t)P(t)+V(t),
P(0)=E\left({{\mathbf {x}}}(0){{\mathbf {x}}}^{{\mathrm T}}(0)\right).

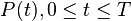Given the solution P(t),0\leq t\leq T the Kalman gain equals,

{{\mathbf {}}}K(t)=P(t)C^{{\mathrm T}}(t)W^{{-1}}(t)

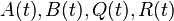The matrix {{\mathbf {}}}L(t) is called the feedback gain matrix. This matrix is determined by the matrices {{\mathbf {}}}A(t),B(t),Q(t),R(t) and {{\mathbf {}}}F through the following associated matrix Riccati differential equation,

-{\dot {S}}(t)=A^{{\mathrm T}}(t)S(t)+S(t)A(t)-S(t)B(t)R^{{-1}}(t)B^{{\mathrm T}}(t)S(t)+Q(t),
{{\mathbf {}}}S(T)=F.

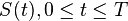Given the solution {{\mathbf {}}}S(t),0\leq t\leq T the feedback gain equals,

{{\mathbf {}}}L(t)=R^{{-1}}(t)B^{{\mathrm T}}(t)S(t).

Observe the similarity of the two matrix Riccati differential equations, the first one running forward in time, the second one running backward in time. This similarity is called duality. The first matrix Riccati differential equation solves the linear-quadratic estimation problem (LQE). The second matrix Riccati differential equation solves the linear-quadratic regulator problem (LQR). These problems are dual and together they solve the linear-quadratic-Gaussian control problem (LQG). So the LQG problem separates into the LQE and LQR problem that can be solved independently. Therefore the LQG problem is called separable.

When 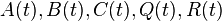{{\mathbf {}}}A(t),B(t),C(t),Q(t),R(t) and the noise intensity matrices 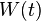{\mathbf {}}V(t), {\mathbf {}}W(t) do not depend on 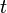{{\mathbf {}}}t and when 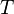{{\mathbf {}}}T tends to infinity the LQG controller becomes a time-invariant dynamic system. In that case both matrix Riccati differential equations may be replaced by the two associated algebraic Riccati equations.

Discrete time

Since the discrete-time LQG control problem is similar to the one in continuous-time the description below focuses on the mathematical equations.

Discrete-time linear system equations:

{{\mathbf {x}}}_{{i+1}}=A_{i}{\mathbf {x}}_{i}+B_{i}{\mathbf {u}}_{i}+{\mathbf {v}}_{i}
{\mathbf {y}}_{{i}}=C_{{i}}{\mathbf {x}}_{i}+{\mathbf {w}}_{i}

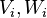Here {\mathbf {}}i represents the discrete time index and {\mathbf {v}}_{{i}},{\mathbf {w}}_{{i}} represent discrete-time Gaussian white noise processes with covariance matrices {\mathbf {}}V_{{i}},W_{{i}} respectively.

The quadratic cost function to be minimized:

J=E\left({{\mathbf {x}}}_{{N}}^{{\mathrm T}}F{{\mathbf {x}}}_{{N}}+\sum _{{i=0}}^{{N-1}}{\mathbf {x}}_{i}^{{\mathrm T}}Q_{i}{\mathbf {x}}_{i}+{\mathbf {u}}_{i}^{{\mathrm T}}R_{i}{\mathbf {u}}_{i}\right),
F\geq 0,Q_{i}\geq 0,R_{i}>0.\,

The discrete-time LQG controller:

{\hat {{\mathbf {x}}}}_{{i+1}}=A_{i}{\hat {{\mathbf {x}}}}_{i}+B_{i}{{\mathbf {u}}}_{i}+K_{i}\left({{\mathbf {y}}}_{i}-C_{i}{{\hat {{\mathbf {x}}}}}_{i}\right),{\hat {{\mathbf {x}}}}_{0}=E({{\mathbf {x}}}_{0}),
{\mathbf {u}}_{i}=-L_{i}{\hat {{\mathbf {x}}}}_{i}.\,

The Kalman gain equals,

{{\mathbf {}}}K_{i}=P_{i}C_{i}^{{\mathrm T}}(C_{i}P_{i}C_{i}^{{\mathrm T}}+W_{i})^{{-1}},

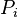where {{\mathbf {}}}P_{i} is determined by the following matrix Riccati difference equation that runs forward in time,

P_{{i+1}}=A_{i}\left(P_{i}-P_{i}C_{i}^{{\mathrm T}}\left(C_{i}P_{i}C_{i}^{{\mathrm T}}+W_{i}\right)^{{-1}}C_{i}P_{i}\right)A_{i}^{{\mathrm T}}+V_{i},P_{0}=E\left({{\mathbf {x}}}_{0}{{\mathbf {x}}}_{0}^{{\mathrm T}}\right).

The feedback gain matrix equals,

{{\mathbf {}}}L_{i}=(B_{i}^{{\mathrm T}}S_{{i+1}}B_{i}+R_{i})^{{-1}}B_{i}^{{\mathrm T}}S_{{i+1}}A_{i}.

where {{\mathbf {}}}S_{i} is determined by the following matrix Riccati difference equation that runs backward in time,

S_{i}=A_{i}^{{\mathrm T}}\left(S_{{i+1}}-S_{{i+1}}B_{i}\left(B_{i}^{{\mathrm T}}S_{{i+1}}B_{i}+R_{i}\right)^{{-1}}B_{i}^{{\mathrm T}}S_{{i+1}}\right)A_{i}+Q_{i},S_{N}=F.

If all the matrices in the problem formulation are time-invariant and if the horizon 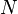{{\mathbf {}}}N tends to infinity the discrete-time LQG controller becomes time-invariant. In that case the matrix Riccati difference equations may be replaced by their associated discrete-time algebraic Riccati equations. These determine the time-invarant linear-quadratic estimator and the time-invariant linear-quadratic regulator in discrete-time. To keep the costs finite instead of 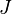{{\mathbf {}}}J one has to consider 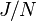{{\mathbf {}}}J/N in this case.

See also

References

  1. ↑ Athans M. (1971). "The role and use of the stochastic Linear-Quadratic-Gaussian problem in control system design". IEEE Transaction on Automatic Control. AC-16 (6): 529–552. doi:10.1109/TAC.1971.1099818. 
  2. ↑ 2.0 2.1 Van Willigenburg L.G., De Koning W.L. (2000). "Numerical algorithms and issues concerning the discrete-time optimal projection equations". European Journal of Control 6 (1): 93–100.  Associated software download from Matlab Central.
  3. ↑ 3.0 3.1 Van Willigenburg L.G., De Koning W.L. (1999). "Optimal reduced-order compensators for time-varying discrete-time systems with deterministic and white parameters". Automatica 35: 129–138. doi:10.1016/S0005-1098(98)00138-1.  Associated software download from Matlab Central.
  4. ↑ Zigic D., Watson L.T., Collins E.G., Haddad W.M., Ying S. (1996). "Homotopy methods for solving the optimal projection equations for the H2 reduced order model problem". International Journal of Control 56 (1): 173–191. doi:10.1080/00207179208934308. 
  5. ↑ Collins Jr. E.G, Haddad W.M., Ying S. (1996). "A homotopy algorithm for reduced-order dynamic compensation using the Hyland-Bernstein optimal projection equations". Journal of Guidance Control & Dynamics 19 (2): 407–417. doi:10.2514/3.21633. 
  6. ↑ Hyland D.C, Bernstein D.S. (1984). "The optimal projection equations for fixed order dynamic compensation". IEEE Transaction on Automatic Control. AC-29 (11): 1034–1037. doi:10.1109/TAC.1984.1103418. 
  7. ↑ Bernstein D.S., Davis L.D., Hyland D.C. (1986). "The optimal projection equations for reduced-order discrete-time modeling estimation and control". Journal of Guidance Control and Dynamics 9 (3): 288–293. doi:10.2514/3.20105. 
  8. ↑ Green, Limebeer: Linear Robust Control, p. 27
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.