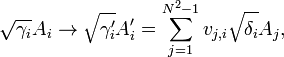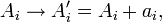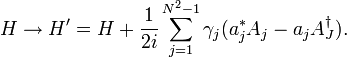Lindblad equation
In quantum mechanics, Kossakowski–Lindblad equation (after Andrzej Kossakowski and Göran Lindblad) or master equation in Lindblad form is the most general type of Markovian and time-homogeneous master equation describing non-unitary evolution of the density matrix  that is trace-preserving and completely positive for any initial condition.
that is trace-preserving and completely positive for any initial condition.
Lindblad master equation for an  -dimensional system's reduced density matrix
-dimensional system's reduced density matrix  can be written:
can be written:
where 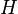 is a (Hermitian) Hamiltonian part, the
is a (Hermitian) Hamiltonian part, the  are an arbitrary orthonormal basis of the operators on the system's Hilbert space, and the
are an arbitrary orthonormal basis of the operators on the system's Hilbert space, and the  are constants which determine the dynamics. The coefficient matrix
are constants which determine the dynamics. The coefficient matrix  must be positive to ensure that the equation is trace-preserving and completely positive. The summation only runs to
must be positive to ensure that the equation is trace-preserving and completely positive. The summation only runs to 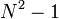 because we have taken
because we have taken  to be proportional to the identity operator, in which case the summand vanishes. Our convention implies that the
to be proportional to the identity operator, in which case the summand vanishes. Our convention implies that the  are traceless for
are traceless for  . The terms in the summation where
. The terms in the summation where 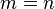 can be described in terms of the Lindblad superoperator,
can be described in terms of the Lindblad superoperator,  .
.
If the  terms are all zero, then this is quantum Liouville equation (for a closed system), which is the quantum analog of the classical Liouville equation. A related equation describes the time evolution of the expectation values of observables, it is given by the Ehrenfest theorem.
terms are all zero, then this is quantum Liouville equation (for a closed system), which is the quantum analog of the classical Liouville equation. A related equation describes the time evolution of the expectation values of observables, it is given by the Ehrenfest theorem.
Note that 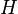 is not necessarily equal to the self-Hamiltonian of the system. It may also incorporate effective unitary dynamics arising from the system-environment interaction.
is not necessarily equal to the self-Hamiltonian of the system. It may also incorporate effective unitary dynamics arising from the system-environment interaction.
Diagonalization
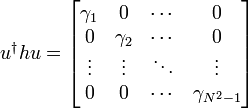
Since the matrix  is positive, it can be diagonalized with a unitary transformation u:
is positive, it can be diagonalized with a unitary transformation u:
where the eigenvalues  are non-negative. If we define another orthonormal operator basis
are non-negative. If we define another orthonormal operator basis
we can rewrite Lindblad equation in diagonal form
This equation is invariant under a unitary transformation of Lindblad operators and constants,
and also under the inhomogenous transformation
However, the first transformation destroys the orthonormality of the operators  (unless all the
(unless all the  are equal) and the second transformation destroys the tracelessness. Therefore, up to degeneracies among the
are equal) and the second transformation destroys the tracelessness. Therefore, up to degeneracies among the  , the
, the  of the diagonal form of the Lindblad equation are uniquely determined by the dynamics so long as we require them to be orthonormal and traceless.
of the diagonal form of the Lindblad equation are uniquely determined by the dynamics so long as we require them to be orthonormal and traceless.
Harmonic oscillator example
The most common Lindblad equation is that describing the damping of a quantum harmonic oscillator, it has 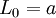 ,
,  ,
,  ,
, 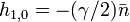 with all others
with all others 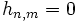 . Here
. Here 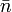 is the mean number of excitations in the reservoir damping the oscillator and
is the mean number of excitations in the reservoir damping the oscillator and  is the decay rate. Additional Lindblad operators can be included to model various forms of dephasing and vibrational relaxation. These methods have been incorporated into grid-based density matrix propagation methods.
is the decay rate. Additional Lindblad operators can be included to model various forms of dephasing and vibrational relaxation. These methods have been incorporated into grid-based density matrix propagation methods.
See also
References
- Kossakowski, A. (1972). "On quantum statistical mechanics of non-Hamiltonian systems". Rep. Math. Phys. 3 (4): 247. Bibcode:1972RpMP....3..247K. doi:10.1016/0034-4877(72)90010-9.
- Lindblad, G. (1976). "On the generators of quantum dynamical semigroups". Commun. Math. Phys. 48 (2): 119. doi:10.1007/BF01608499.
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. (1976). "Completely positive semigroups of N-level systems". J. Math. Phys. 17 (5): 821. doi:10.1063/1.522979.
- Banks, T.; Susskind, L.; Peskin, M.E. (1984). "Difficulties for the evolution of pure states into mixed states". Nuclear Physics B 244: 125–134. Bibcode:1984NuPhB.244..125B. doi:10.1016/0550-3213(84)90184-6.
- Accardi, Luigi; Lu, Yun Gang; Volovich, I.V. (2002). Quantum Theory and Its Stochastic Limit. New York: Springer Verlag. ISBN 978-3-5404-1928-0.
- Alicki, Robert; Lendi, Karl (1987). Quantum Dynamical Semigroups and Applications. Berlin: Springer Verlag. ISBN 978-0-3871-8276-6.
- Attal, Stéphane; Joye, Alain; Pillet, Claude-Alain (2006). Open Quantum Systems II: The Markovian Approach. Springer. ISBN 978-3-5403-0992-5.
- Breuer, Heinz-Peter; Petruccione, F. (2002). The Theory of Open Quantum Systems. Oxford University Press. ISBN 978-0-1985-2063-4.
- Gardiner, C.W.; Zoller, Peter (2010). Quantum Noise. Springer Series in Synergetics (3rd ed.). Berlin Heidelberg: Springer-Verlag. ISBN 978-3-642-06094-6.
- Ingarden, Roman S.; Kossakowski, A.; Ohya, M. (1997). Information Dynamics and Open Systems: Classical and Quantum Approach. New York: Springer Verlag. ISBN 978-0-7923-4473-5.
- Lindblad, G. (1983). Non-Equilibrium Entropy and Irreversibility. Dordrecht: Delta Reidel. ISBN 1-4020-0320-X.
- Tarasov, Vasily E. (2008). Quantum Mechanics of Non-Hamiltonian and Dissipative Systems. Amsterdam, Boston, London, New York: Elsevier Science. ISBN 978-0-0805-5971-1.
![{\dot \rho }=-{i \over \hbar }[H,\rho ]+\sum _{{n,m=1}}^{{N^{2}-1}}h_{{n,m}}{\big (}L_{n}\rho L_{m}^{\dagger }-{\frac {1}{2}}\left(\rho L_{m}^{\dagger }L_{n}+L_{m}^{\dagger }L_{n}\rho \right){\big )}](/2014-wikipedia_en_all_02_2014/I/media/f/4/f/3/f4f3d0e7c1547bebc35f258e7fc62f43.png)
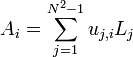
![{\dot \rho }=-{i \over \hbar }[H,\rho ]+\sum _{{i=1}}^{{N^{2}-1}}\gamma _{{i}}{\big (}A_{i}\rho A_{i}^{\dagger }-{\frac {1}{2}}\rho A_{i}^{\dagger }A_{i}-{\frac {1}{2}}A_{i}^{\dagger }A_{i}\rho {\big )}.](/2014-wikipedia_en_all_02_2014/I/media/b/f/5/7/bf570ab1c29dbbdf240580ee0cb32e80.png)