Lightface analytic game

From Wikipedia, the free encyclopedia

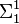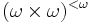In descriptive set theory, a lightface analytic game is a game whose payoff set A is a $\Sigma _{1}^{1}$ subset of Baire space; that is, there is a tree T on $\omega \times \omega$ which is a computable subset of $(\omega \times \omega )^{{<\omega }}$ , such that A is the projection of the set of all branches of T.

The determinacy of all lightface analytic games is equivalent to the existence of 0^#.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.