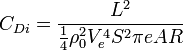Lift-induced drag

From Wikipedia, the free encyclopedia

In aerodynamics, lift-induced drag, induced drag, vortex drag, or sometimes drag due to lift, is a drag force that occurs whenever a moving object redirects the airflow coming at it. This drag force occurs in airplanes due to wings or a lifting body redirecting air to cause lift and also in cars with airfoil wings that redirect air to cause a downforce. With other parameters remaining the same, induced drag increases as the angle of attack increases.^[4]

Source of induced drag

Induced drag is related to the amount of induced downwash in the vicinity of the wing. The grey vertical line labeled "L" is perpendicular to the free stream and indicates the orientation of the lift on the wing. The red vector labeled "L_eff" is perpendicular to the actual airflow in the vicinity of the wing; it represents the lift on the airfoil section in two–dimensional flow at the same angle of attack. The lift generated by the wing has been tilted rearwards through an angle equal to the angle of the downwash in three-dimensional flow. The component of "L_eff" parallel to the free stream is the induced drag on the wing.^[1]^[2]^[3]

Lift is produced by the changing direction of the flow around a wing. The change of direction results in a change of velocity (even if there is no speed change, just as seen in uniform circular motion), which is an acceleration. To change the direction of the flow therefore requires that a force be applied to the fluid; lift is simply the reaction force of the fluid acting on the wing.

When producing lift, air below the wing is generally at a higher pressure than the air pressure above the wing, while air above the wing is generally at a lower than atmospheric pressure. On a wing of finite span, this pressure difference causes air to flow from the lower surface wing root, around the wingtip, towards the upper surface wing root. This spanwise flow of air combines with chordwise flowing air, causing a change in speed and direction, which twists the airflow and produces vortices along the wing trailing edge. The vortices created are unstable, and they quickly combine to produce wingtip vortices.^[5] The resulting vortices change the speed and direction of the airflow behind the trailing edge, deflecting it downwards, and thus inducing downwash behind the wing.

Wingtip vortices modify the airflow around a wing. Compared to a wing of infinite span, vortices reduce the effectiveness of the wing to generate lift, thus requiring a higher angle of attack to compensate, which tilts the total aerodynamic force rearwards. The angular deflection is small and has little effect on the lift. However, there is an increase in the drag equal to the product of the lift force and the angle through which it is deflected. Since the deflection is itself a function of the lift, the additional drag is proportional to the square of the lift.^[4]

The total aerodynamic force is usually thought of as two components, lift and drag. By definition, the component of force parallel to the oncoming flow is called drag; and the component perpendicular to the oncoming flow is called lift.^[6] At practical angles of attack the lift greatly exceeds the drag.^[7]

Reducing induced drag

According to the equations below, a wing of infinite aspect ratio (wingspan/chord length) and constant airfoil section would seemingly produce no induced drag per unit of surface area (although this depends on what happens to the factor e). The characteristics of such a wing can be measured on a section of wing spanning the width of a wind tunnel, since the walls block spanwise flow and create what is effectively two-dimensional flow. However, in reality, there will still be more drag (induced drag) when the angle of attack is high than when it is zero or slightly negative.

A rectangular wing produces much more severe wingtip vortices than a tapered or elliptical wing, therefore many modern wings are tapered. However, an elliptical planform is more efficient as the induced downwash (and therefore the effective angle of attack) is constant across the whole of the wingspan. Few aircraft have this planform because of manufacturing complications — the most famous examples being the World War II Spitfire and Thunderbolt. Tapered wings with straight leading and trailing edges can approximate to elliptical lift distribution. Typically, straight wings produce between 5–15% more induced drag than an elliptical wing.

Similarly, a high aspect ratio wing will produce less induced drag than a wing of low aspect ratio because the size of the wing vortices will be much reduced on a longer, thinner wing. Induced drag can therefore be said to be inversely proportional to aspect ratio. The lift distribution may also be modified by the use of washout, a spanwise twist of the wing to reduce the incidence towards the wingtips, and by changing the airfoil section near the wingtips. This allows more lift to be generated at the wing root and less towards the wingtip, which causes a reduction in the strength of the wingtip vortices.

Some early aircraft had fins mounted on the tips of the tailplane which served as endplates. More recent aircraft have wingtip mounted winglets or wing fences to oppose the formation of vortices. Wingtip mounted fuel tanks may also provide some benefit, by preventing the spanwise flow of air around the wingtip.

Calculation of induced drag

Lift and Drag curves for a typical airfoil

For a planar wing wing with an elliptical lift distribution, induced drag is often calculated as follows. These equations make the induced drag depend on the square of the lift, for a given aspect ratio and surface area (while varying the angle of attack), but as the accompanying graph shows, this is only an approximation and is not valid at high angles of attack (and probably not for very high values of aspect ratio either).

$D_{i}={\frac {1}{2}}\rho V^{2}SC_{{Di}}={\frac {1}{2}}\rho _{0}V_{e}^{2}SC_{{Di}}$

where

$C_{{Di}}={\frac {C_{L}^{2}}{\pi eAR}}$ and

$C_{L}={\frac {L}{{\frac {1}{2}}\rho _{0}V_{e}^{2}S}}$

Thus

$C_{{Di}}={\frac {L^{2}}{{\frac {1}{4}}\rho _{0}^{2}V_{e}^{4}S^{2}\pi eAR}}$

Hence

$D_{i}={\frac {L^{2}}{{\frac {1}{2}}\rho _{0}V_{e}^{2}S\pi eAR}}$

Where:

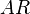$AR\,$ is the aspect ratio,

$C_{{Di}}\,$ is the induced drag coefficient (see Lifting-line theory),

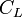$C_{L}\,$ is the lift coefficient,

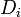$D_{i}\,$ is the induced drag,

$e\,$ is the wing span efficiency value by which the induced drag exceeds that of an elliptical lift distribution, typically 0.85 to 0.95,

$L\,$ is the lift,

$S\,$ is the gross wing area: the product of the wing span and the Mean Aerodynamic Chord.

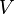$V\,$ is the true airspeed,

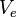$V_{e}\,$ is the equivalent airspeed,

$\rho \,$ is the air density and

$\rho _{0}\,$ is 1.225 kg/m³, the air density at sea level, ISA conditions.

Combined effect with other drag sources

Induced drag must be added to the parasitic drag to find the total drag. Since induced drag is inversely proportional to the square of the airspeed (at a given lift) whereas parasitic drag is proportional to the square of the airspeed, the combined overall drag curve shows a minimum at some airspeed - the minimum drag speed (V_MD). An aircraft flying at this speed is at its optimal aerodynamic efficiency. According to the above equations, the minimum drag speed occurs at the speed where the induced drag is equal to the parasitic drag. This is the speed at which the best gradient of climb, or for unpowered aircraft, minimum gradient of descent, is achieved.^[8] This is also the speed for greatest range (although V_MD will decrease as the plane consumes fuel and becomes lighter). The speed for greatest range (i.e., distance travelled) is the speed at which a straight line from the origin is tangent to the fuel flow rate curve. The curve of range versus airspeed is normally very flat and it is customary to operate at the speed for 99% best range since this gives about 5% greater speed for only 1% less range. (Of course, flying higher where the air is thinner will raise the speed of minimum drag, and so permits a faster voyage for the same amount of fuel. If the plane is flying at the maximum permissible speed, then there is an altitude at which the air density will be what is needed to keep it aloft while flying at the angle of attack that minimizes the drag. The optimum altitude at maximum speed, and the optimum speed at maximum altitude, may change during the flight as the plane becomes lighter.)

The speed for best endurance (i.e., time in the air) is the speed for minimum fuel flow rate, and is less than the speed for greatest range. The fuel flow rate is calculated as the product of the power required and the engine specific fuel consumption (fuel flow rate per unit of power^[9]). The power required is equal to the drag times the speed.

Minimum induced drag for generic non-planar systems

The problem is translated in finding the optimal circulation distribution which minimizes the induced drag for a given wingspan and total lift. The concepts of Optimal Aerodynamic Efficiency Ratio, Augmented Munk's Minimum Induced Drag Theorem, Minimum Induced Drag Curvature-Invariance Theorem, and Quasi-Closed C-Wing Zero Gradient Optimal Circulation Theorem are now discussed.

Optimal aerodynamic efficiency ratio

The optimal aerodynamic efficiency ratio for a given wing represents the ratio between its aerodynamic efficiency and the corresponding efficiency of a reference classical cantilevered wing with the same wing span and total lift. Both efficiencies are evaluated under their respective optimal conditions.^[10]

The optimal aerodynamic efficiency ratio should not be confused with the wing span efficiency value e.

Optimal Aerodynamic Efficiency Ratio

Augmented Munk's minimum induced drag theorem

When the lifting system has been translated into a single plane (Munk's stagger theorem), the induced drag will be minimum when the component of the induced velocity normal to the lifting element at each point is proportional to the cosine of the angle of inclination of the lifting element at that point.^[11] The constant of proportionality is the ratio between the freestream velocity and the optimal aerodynamic efficiency.^[12]

Augmented Munk's Minimum Induced Drag Theorem

Minimum induced drag curvature-invariance theorem

Changing the sign of the curvature of the lifting line (i.e., the arc from convex is changed to concave or viceversa) does not modify the optimal induced drag and circulation distribution: the optimal solution is then invariant if the sign of the curvature is modified.^[13]

Minimum Induced Drag Curvature-Invariance Theorem

Quasi-closed C-wing zero gradient optimal circulation theorem

If the two tips of a C wing are brought indefinitely close to each other, then both the optimal circulation and its first derivative tend to zero at those points.^[14]

Quasi-Closed C-Wing Zero Gradient Optimal Circulation Theorem

Optimal induced drag: minimization procedure and results

The optimal conditions are found by solving an integral equation (see figure). Several non-planar wings are presented.

Minimum Induced Drag: Procedure

Nonplanar wings: results

References

Clancy, L.J. (1975), Aerodynamics, Pitman Publishing Limited, London. ISBN 0-273-01120-0
Abbott, Ira H., and Von Doenhoff, Albert E. (1959), Theory of Wing Sections, Dover Publications Inc., New York, Standard Book Number 486-60586-8
Demasi Luciano, Dipace Antonio, Monegato Giovanni, Cavallaro Rauno An Invariant Formulation for the Minimum Induced Drag Conditions of Non-planar Wing Systems, AIAA Journal, in press (2014)

Notes

↑ Hurt, H. H. (1965) Aerodynamics for Naval Aviators, Figure 1.30, NAVWEPS 00-80T-80
↑ Clancy, L.J. (1975) Aerodynamics Fig 5.24. Pitman Publishing Limited, London. ISBN 0-273-01120-0
↑ Kermode, A.C. (1972). Mechanics of Flight, Figure 3.29, Ninth edition. Longman Scientific & Technical, England. ISBN 0-582-42254-X
↑ 4.0 4.1 Clancy, L.J., Aerodynamics, Section 5.17
↑ Clancy, L.J., Aerodynamics, Section 5.14
↑ Clancy, L.J., Aerodynamics, Section 5.3
↑ Abbott, Ira H., and Von Doenhoff, Albert E., Theory of Wing Sections, Section 1.2 and Appendix IV
↑ Clancy, L.J., Aerodynamics, Section 5.25
↑ The engine specific fuel consumption is normally expressed in units of fuel flow rate per unit of thrust or per unit of power depending on whether the engine output is measured in thrust, as for a jet engine, or power, as for a turbo-prop engine. To convert fuel rate per unit thrust to fuel rate per unit power one must divide by the speed.
↑ Demasi Luciano, Dipace Antonio, Monegato Giovanni, Cavallaro Rauno, An Invariant Formulation for the Minimum Induced Drag Conditions of Non-planar Wing Systems, AIAA Journal, in press (2014); sections VII and VIII
↑ M. Munk, The Minimum Induced Drag in Airfoils, NACA Report 121, 1921
↑ Demasi Luciano, Dipace Antonio, Monegato Giovanni, Cavallaro Rauno An Invariant Formulation for the Minimum Induced Drag Conditions of Non-planar Wing Systems, AIAA Journal, in press (2014); Section V
↑ Demasi Luciano, Dipace Antonio, Monegato Giovanni, Cavallaro Rauno, An Invariant Formulation for the Minimum Induced Drag Conditions of Non-planar Wing Systems, AIAA Journal, in press (2014); Section IX
↑ Demasi Luciano, Dipace Antonio, Monegato Giovanni, Cavallaro Rauno, An Invariant Formulation for the Minimum Induced Drag Conditions of Non-planar Wing Systems, AIAA Journal, in press (2014); Section X

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.