Lie groupoid
In mathematics, a Lie groupoid is a groupoid where the set 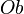 of objects and the set
of objects and the set 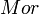 of morphisms are both manifolds, the source and target operations
of morphisms are both manifolds, the source and target operations
are submersions, and all the category operations (source and target, composition, and identity-assigning map) are smooth.
A Lie groupoid can thus be thought of as a "many-object generalization" of a Lie group, just as a groupoid is a many-object generalization of a group. Just as every Lie group has a Lie algebra, every Lie groupoid has a Lie algebroid.
Examples
- Any Lie group gives a Lie groupoid with one object, and conversely. So, the theory of Lie groupoids includes the theory of Lie groups.
- Given any manifold
 , there is a Lie groupoid called the pair groupoid, with
, there is a Lie groupoid called the pair groupoid, with  as the manifold of objects, and precisely one morphism from any object to any other. In this Lie groupoid the manifold of morphisms is thus
as the manifold of objects, and precisely one morphism from any object to any other. In this Lie groupoid the manifold of morphisms is thus 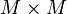 .
.
- Given a Lie group
 acting on a manifold
acting on a manifold  , there is a Lie groupoid called the translation groupoid with one morphism for each triple
, there is a Lie groupoid called the translation groupoid with one morphism for each triple 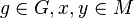 with
with  .
.
- Any foliation gives a Lie groupoid.
- Any principal bundle
 with structure group G gives a groupoid, namely
with structure group G gives a groupoid, namely  over M, where G acts on the pairs componentwise. Composition is defined via compatible representatives as in the pair groupoid.
over M, where G acts on the pairs componentwise. Composition is defined via compatible representatives as in the pair groupoid.
Morita Morphisms and Smooth Stacks
Beside isomorphism of groupoids there is a more coarse notation of equivalence, the so-called Morita equivalence. A quite general example is the Morita-morphism of the Čech groupoid which goes as follows. Let M be a smooth manifold and  an open cover of M. Define
an open cover of M. Define  the disjoint union with the obvious submersion
the disjoint union with the obvious submersion  . In order to encode the structure of the manifold M define the set of morphisms
. In order to encode the structure of the manifold M define the set of morphisms 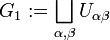 where
where 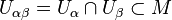 . The source and target map are defined as the embeddings
. The source and target map are defined as the embeddings  and
and  . And multiplication is the obvious one if we read the
. And multiplication is the obvious one if we read the  as subsets of M (compatible points in
as subsets of M (compatible points in  and
and  actually are the same in M and also lie in
actually are the same in M and also lie in 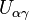 ).
).
This Čech groupoid is in fact the pullback groupoid of 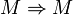 , i.e. the trivial groupoid over M, under p. That is what makes it Morita-morphism.
, i.e. the trivial groupoid over M, under p. That is what makes it Morita-morphism.
In order to get the notion of an equivalence relation we need to make the construction symmetric and show that it is also transitive. In this sense we say that 2 groupoids  and
and 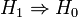 are Morita equivalent iff there exists a third groupoid
are Morita equivalent iff there exists a third groupoid 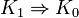 together with 2 Morita morphisms from G to K and H to K. Transitivity is an interesting construction in the category of groupoid principal bundles and left to the reader.
together with 2 Morita morphisms from G to K and H to K. Transitivity is an interesting construction in the category of groupoid principal bundles and left to the reader.
It arises the question of what is preserved under the Morita equivalence. There are 2 obvious things, one the coarse quotient/ orbit space of the groupoid  and secondly the stabilizer groups
and secondly the stabilizer groups  for corresponding points
for corresponding points 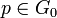 and
and 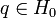 .
.
The further question of what is the structure of the coarse quotient space leads to the notion of a smooth stack. We can expect the coarse quotient to be a smooth manifold if for example the stabilizer groups are trivial (as in the example of the Čech groupoid). But if the stabilizer groups change we cannot expect a smooth manifold any longer. The solution is to revert the problem and to define:
A smooth stack is a Morita-equivalence class of Lie groupoids. The natural geometric objects living on the stack are the geometric objects on Lie groupoids invariant under Morita-equivalence. As an example consider the Lie groupoid cohomology.
Examples
- The notion of smooth stack is quite general, obviously all smooth manifolds are smooth stacks.
- But also orbifolds are smooth stacks, namely (equivalence classes of) étale groupoids.
- Orbit spaces of foliations are another class of examples
External links
Alan Weinstein, Groupoids: unifying internal and external symmetry, AMS Notices, 43 (1996), 744-752. Also available as arXiv:math/9602220
Kirill Mackenzie, Lie Groupoids and Lie Algebroids in Differential Geometry, Cambridge U. Press, 1987.
Kirill Mackenzie, General Theory of Lie Groupoids and Lie Algebroids, Cambridge U. Press, 2005
