Lie coalgebra
In mathematics a Lie coalgebra is the dual structure to a Lie algebra.
In finite dimensions, these are dual objects: the dual vector space to a Lie algebra naturally has the structure of a Lie coalgebra, and conversely.
Definition
Let E be a vector space over a field k equipped with a linear mapping 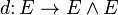 from E to the exterior product of E with itself. It is possible to extend d uniquely to a graded derivation (this means that, for any a, b ∈ E which are homogeneous elements,
from E to the exterior product of E with itself. It is possible to extend d uniquely to a graded derivation (this means that, for any a, b ∈ E which are homogeneous elements,  ) of degree 1 on the exterior algebra of E:
) of degree 1 on the exterior algebra of E:
Then the pair (E, d) is said to be a Lie coalgebra if d2 = 0,
i.e., if the graded components of the exterior algebra with derivation 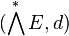 form a cochain complex:
form a cochain complex:
Relation to de Rham complex
Just as the exterior algebra (and tensor algebra) of vector fields on a manifold form a Lie algebra (over the base field K), the de Rham complex of differential forms on a manifold form a Lie coalgebra (over the base field K). Further, there is a pairing between vector fields and differential forms.
However, the situation is subtler: the Lie bracket is not linear over the algebra of smooth functions 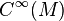 (the error is the Lie derivative), nor is the exterior derivative:
(the error is the Lie derivative), nor is the exterior derivative: 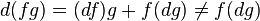 (it is a derivation, not linear over functions): they are not tensors. They are not linear over functions, but they behave in a consistent way, which is not captured simply by the notion of Lie algebra and Lie coalgebra.
(it is a derivation, not linear over functions): they are not tensors. They are not linear over functions, but they behave in a consistent way, which is not captured simply by the notion of Lie algebra and Lie coalgebra.
Further, in the de Rham complex, the derivation is not only defined for 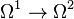 , but is also defined for
, but is also defined for 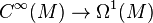 .
.
The Lie algebra on the dual
A Lie algebra structure on a vector space is a map ![[\cdot ,\cdot ]\colon {\mathfrak {g}}\times {\mathfrak {g}}\to {\mathfrak {g}}](/2014-wikipedia_en_all_02_2014/I/media/e/9/4/9/e949d4e54ff8079250d0f131c43ddd98.png) which is skew-symmetric, and satisfies the Jacobi identity. Equivalently, a map
which is skew-symmetric, and satisfies the Jacobi identity. Equivalently, a map ![[\cdot ,\cdot ]\colon {\mathfrak {g}}\wedge {\mathfrak {g}}\to {\mathfrak {g}}](/2014-wikipedia_en_all_02_2014/I/media/d/1/a/b/d1ab2e8b5610c74b5435cbd442c24629.png) that satisfies the Jacobi identity.
that satisfies the Jacobi identity.
Dually, a Lie coalgebra structure on a vector space E is a linear map 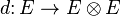 which is antisymmetric (this means that it satisfies
which is antisymmetric (this means that it satisfies  , where
, where  is the canonical flip
is the canonical flip  ) and satisfies the so-called cocycle condition (also known as the co-Leibniz rule)
) and satisfies the so-called cocycle condition (also known as the co-Leibniz rule)
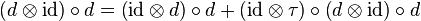 .
.
Due to the antisymmetry condition, the map 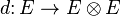 can be also written as a map
can be also written as a map 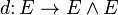 .
.
The dual of the Lie bracket of a Lie algebra  yields a map (the cocommutator)
yields a map (the cocommutator)
where the isomorphism 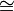 holds in finite dimension; dually for the dual of Lie comultiplication. In this context, the Jacobi identity corresponds to the cocycle condition.
holds in finite dimension; dually for the dual of Lie comultiplication. In this context, the Jacobi identity corresponds to the cocycle condition.
More explicitly, let E be a Lie coalgebra over a field of characteristic neither 2 nor 3. The dual space E* carries the structure of a bracket defined by
- α([x, y]) = dα(x∧y), for all α ∈ E and x,y ∈ E*.
We show that this endows E* with a Lie bracket. It suffices to check the Jacobi identity. For any x, y, z ∈ E* and α ∈ E,
where the latter step follows from the standard identification of the dual of a wedge product with the wedge product of the duals. Finally, this gives
Since d2 = 0, it follows that
![\alpha ([[x,y],z]+[[y,z],x]+[[z,x],y])=0](/2014-wikipedia_en_all_02_2014/I/media/8/1/d/7/81d7ae1441ca0f4fd632dca64814a6a7.png) , for any α, x, y, and z.
, for any α, x, y, and z.
Thus, by the double-duality isomorphism (more precisely, by the double-duality monomorphism, since the vector space needs not be finite-dimensional), the Jacobi identity is satisfied.
In particular, note that this proof demonstrates that the cocycle condition d2 = 0 is in a sense dual to the Jacobi identity.
References
- Michaelis, Walter (1980), "Lie coalgebras", Advances in Mathematics 38 (1): 1–54, doi:10.1016/0001-8708(80)90056-0, ISSN 0001-8708, MR 594993

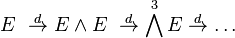
![[\cdot ,\cdot ]^{*}\colon {\mathfrak {g}}^{*}\to ({\mathfrak {g}}\wedge {\mathfrak {g}})^{*}\cong {\mathfrak {g}}^{*}\wedge {\mathfrak {g}}^{*}](/2014-wikipedia_en_all_02_2014/I/media/7/5/9/2/759209167cb7df7bf916b7f24fec68cc.png)
![d^{2}\alpha (x\wedge y\wedge z)={\frac {1}{3}}d^{2}\alpha (x\wedge y\wedge z+y\wedge z\wedge x+z\wedge x\wedge y)={\frac {1}{3}}\left(d\alpha ([x,y]\wedge z)+d\alpha ([y,z]\wedge x)+d\alpha ([z,x]\wedge y)\right),](/2014-wikipedia_en_all_02_2014/I/media/b/a/3/f/ba3f2f7a0595b224a461e33c25dfa43c.png)
![d^{2}\alpha (x\wedge y\wedge z)={\frac {1}{3}}\left(\alpha ([[x,y],z])+\alpha ([[y,z],x])+\alpha ([[z,x],y])\right).](/2014-wikipedia_en_all_02_2014/I/media/1/d/4/4/1d44abf2bb96de234a7003e9c5a4bf81.png)