Lie bialgebra
In mathematics, a Lie bialgebra is the Lie-theoretic case of a bialgebra: it's a set with a Lie algebra and a Lie coalgebra structure which are compatible.
It is a bialgebra where the comultiplication is skew-symmetric and satisfies a dual Jacobi identity, so that the dual vector space is a Lie algebra, whereas the comultiplication is a 1-cocycle, so that the multiplication and comultiplication are compatible. The cocycle condition implies that, in practice, one studies only classes of bialgebras that are cohomologous to a Lie bialgebra on a coboundary.
They are also called Poisson-Hopf algebras, and are the Lie algebra of a Poisson-Lie group.
Lie bialgebras occur naturally in the study of the Yang-Baxter equations.
Definition
More precisely, comultiplication on the algebra, 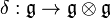 , is called the cocommutator, and must satisfy two properties. The dual
, is called the cocommutator, and must satisfy two properties. The dual
must be a Lie bracket on 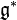 , and it must be a cocycle:
, and it must be a cocycle:
where ![\operatorname {ad}_{X}Y=[X,Y]](/2014-wikipedia_en_all_02_2014/I/media/6/1/8/e/618e0a91b2ab7ac164a43c1621f70cbd.png) is the adjoint.
is the adjoint.
Relation to Poisson-Lie groups
Let G be a Poisson-Lie group, with 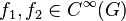 being two smooth functions on the group manifold. Let
being two smooth functions on the group manifold. Let  be the differential at the identity element. Clearly,
be the differential at the identity element. Clearly, 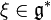 . The Poisson structure on the group then induces a bracket on
. The Poisson structure on the group then induces a bracket on 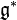 , as
, as
where  is the Poisson bracket. Given
is the Poisson bracket. Given  be the Poisson bivector on the manifold, define
be the Poisson bivector on the manifold, define 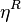 to be the right-translate of the bivector to the identity element in G. Then one has that
to be the right-translate of the bivector to the identity element in G. Then one has that
The cocommutator is then the tangent map:
so that
is the dual of the cocommutator.
See also
References
- H.-D. Doebner, J.-D. Hennig, eds, Quantum groups, Proceedings of the 8th International Workshop on Mathematical Physics, Arnold Sommerfeld Institute, Claausthal, FRG, 1989, Springer-Verlag Berlin, ISBN 3-540-53503-9.
- Vyjayanthi Chari and Andrew Pressley, A Guide to Quantum Groups, (1994), Cambridge University Press, Cambridge ISBN 0-521-55884-0.
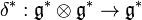
![\delta ([X,Y])=\left(\operatorname {ad}_{X}\otimes 1+1\otimes \operatorname {ad}_{X}\right)\delta (Y)-\left(\operatorname {ad}_{Y}\otimes 1+1\otimes \operatorname {ad}_{Y}\right)\delta (X)](/2014-wikipedia_en_all_02_2014/I/media/3/5/4/1/35417ed30a50b976c9bb4f793e1148fd.png)
![[\xi _{1},\xi _{2}]=(d\{f_{1},f_{2}\})_{e}\,](/2014-wikipedia_en_all_02_2014/I/media/2/c/7/d/2c7d86540e113da19fc5e35acc010422.png)
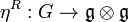
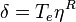
![[\xi _{1},\xi _{2}]=\delta ^{*}(\xi _{1}\otimes \xi _{2})](/2014-wikipedia_en_all_02_2014/I/media/f/4/1/b/f41b0b235c0e364e7bd1172824c67a68.png)