Leray cover

From Wikipedia, the free encyclopedia

In mathematics, a Leray cover(ing) is a cover which allows for easy calculation of cohomology.

Sheaf cohomology measures the extent to which a locally exact sequence on a fixed topological space, for instance the deRham sequence, fails to be globally exact. Its definition, using derived functors, is reasonably natural, if technical. Moreover, important properties, such as the existence of a long exact sequence in cohomology corresponding to any short exact sequence of sheaves, follow directly from the definition. However, it is virtually impossible to calculate from the definition. On the other hand, Čech cohomology with respect to an open cover is well-suited to calculation, but of limited usefulness because it depends on the open cover chosen, not only on the sheaves and the space. By taking a direct limit of Čech cohomology over arbitrarily fine covers, we obtain a Čech cohomology theory that does not depend on the open cover chosen. In reasonable circumstances (for instance, if the topological space is paracompact), the derived-functor cohomology agrees with this Ĉech cohomology obtained by direct limits. However, like the derived functor cohomology, this cover-independent Čech cohomology is virtually impossible to calculate from the definition. The Leray condition on an open cover ensures that the cover in question is already "fine enough." The derived functor cohomology agrees with the Čech cohomology with respect to any Leray cover.

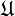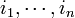Let ${\mathfrak {U}}=\{U_{i}\}$ be an open cover of the topological space $X$ , and ${\mathcal {F}}$ a sheaf on X. We say that ${\mathfrak {U}}$ is a Leray cover with respect to ${\mathcal {F}}$ if, for every nonempty finite set $i_{1},\cdots ,i_{n}$ of indices, and for all 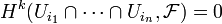$k>0$ , $H^{k}(U_{{i_{1}}}\cap \cdots \cap U_{{i_{n}}},{\mathcal {F}})=0$ , in the derived functor cohomology.^[1] For example, if X is a separated scheme, and ${\mathcal {F}}$ is quasicoherent, then any cover of X by open affine subschemes is a Leray cover.^[2]

References

↑ Taylor, J. L. Several complex variables with connections to algebraic geometry and Lie groups. Graduate Studies in Mathematics v. 46. American Mathematical Society, Providence, RI. 2002.
↑ Macdonald, I. G. Algebraic geometry. Introduction to schemes. W. A. Benjamin, Inc., New York-Amsterdam 1968 vii+113 pp.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.