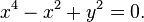Lemniscate of Gerono

From Wikipedia, the free encyclopedia

The lemniscate of Gerono

In algebraic geometry, the lemniscate of Gerono, or lemnicate of Huygens, or figure-eight curve, is a plane algebraic curve of degree four and genus zero and is a lemniscate curve shaped like an $\infty$ symbol, or figure eight. It has equation

$x^{4}-x^{2}+y^{2}=0.$

It was studied by Camille-Christophe Gerono.

Because the curve is of genus zero, it can be parametrized by rational functions; one means of doing that is

$x={\frac {t^{2}-1}{t^{2}+1}},\ y={\frac {2t(t^{2}-1)}{(t^{2}+1)^{2}}}.$

Another representation is

$x=\cos \varphi ,\ y=\sin \varphi \,\cos \varphi =\sin(2\varphi )/2$

which reveals that this lemniscate is a special case of a lissajous figure.

The dual curve (see Plücker formula), pictured below, has therefore a somewhat different character. Its equation is

$(x^{2}-y^{2})^{3}+8y^{4}+20x^{2}y^{2}-x^{4}-16y^{2}=0.$

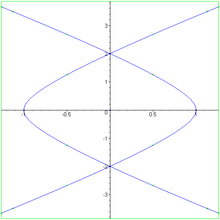
Dual to the lemniscate of Gerono

References

J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. p. 124. ISBN 0-486-60288-5.

Notes

External links

O'Connor, John J.; Robertson, Edmund F., "Figure Eight Curve", MacTutor History of Mathematics archive, University of St Andrews .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.