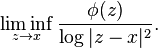Lelong number

From Wikipedia, the free encyclopedia

In mathematics, the Lelong number is an invariant of a point of a complex analytic variety that in some sense measures the local density at that point. It was introduced by Lelong (1957). More generally a closed positive (p,p) current u on a complex manifold has a Lelong number n(u,x) for each point x of the manifold. Similarly a plurisubharmonic function also has a Lelong number at a point.

Definitions

The Lelong number of a plurisubharmonic function φ at a point x of Cⁿ is

$\liminf _{{z\rightarrow x}}{\frac {\phi (z)}{\log |z-x|^{2}}}.$

For a point x of an analytic subset A of pure dimension k, the Lelong number ν(A,x) is the limit of the ratio of the areas of A ∩ B(r,x) and a ball of radius r in C^k as the radius tends to zero. (Here B(r,x) is a ball of radius r centered at x.) In other words the Lelong number is a sort of measure of the local density of A near x. If x is not in the subvariety A the Lelong number is 0, and if x is a regular point the Lelong number is 1. Thie proved that the Lelong number ν(A,x) is always an integer.

References

Lelong, Pierre (1957), "Intégration sur un ensemble analytique complexe", Bulletin de la Société Mathématique de France 85: 239–262, ISSN 0037-9484, MR 0095967
Lelong, Pierre (1968), Fonctions plurisousharmoniques et formes différentielles positives, Paris: Gordon & Breach, MR 0243112
Varolin, Dror (2010), "Three variations on a theme in complex analytic geometry", in McNeal, Jeffery; Mustaţă, Mircea, Analytic and algebraic geometry, IAS/Park City Math. Ser. 17, Providence, R.I.: American Mathematical Society, pp. 183–294, ISBN 978-0-8218-4908-8, MR 2743817

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.