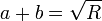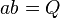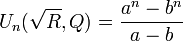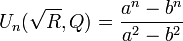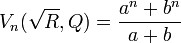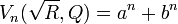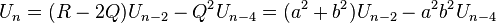Lehmer number
From Wikipedia, the free encyclopedia
In mathematics, a Lehmer number is a generalization of a Lucas sequence.
Algebraic relations
If a and b are complex numbers with
under the following conditions:
- Q and R are relatively prime nonzero integers
-
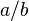 is not a root of unity.
is not a root of unity.
Then, the corresponding Lehmer numbers are:
for n odd, and
for n even.
Their companion numbers are:
for n odd and
for n even.
Recurrence
Lehmer numbers form a linear recurrence relation with
with initial values 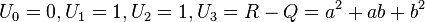 . Similarly the companions sequence satisfies
. Similarly the companions sequence satisfies
with initial values  .
.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.