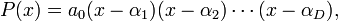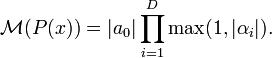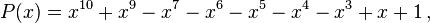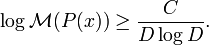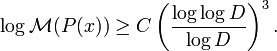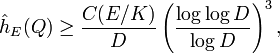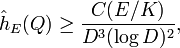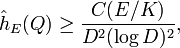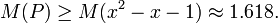Lehmer's conjecture

From Wikipedia, the free encyclopedia

For Lehmer's conjecture about Euler's totient function, see Lehmer's totient problem.

Lehmer's conjecture, also known as the Lehmer's Mahler measure problem, is a problem in number theory raised by Derrick Henry Lehmer.^[1] The conjecture asserts that there is an absolute constant 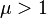$\mu >1$ such that every polynomial with integer coefficients $P(x)\in {\mathbb {Z}}[x]$ satisfies one of the following properties:

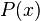The Mahler measure ${\mathcal {M}}(P(x))$ of $P(x)$ is greater than or equal to $\mu$ .

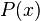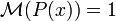$P(x)$ is an integral multiple of a product of cyclotomic polynomials or the monomial $x$ , in which case ${\mathcal {M}}(P(x))=1$ . (Equivalently, every complex root of 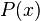$P(x)$ is a root of unity or zero.)

There are a number of definitions of the Mahler measure, one of which is to factor 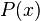$P(x)$ over ${\mathbb {C}}$ as

$P(x)=a_{0}(x-\alpha _{1})(x-\alpha _{2})\cdots (x-\alpha _{D}),$

and then set

${\mathcal {M}}(P(x))=|a_{0}|\prod _{{i=1}}^{{D}}\max(1,|\alpha _{i}|).$

The smallest known Mahler measure (greater than 1) is for "Lehmer's polynomial"

$P(x)=x^{{10}}+x^{9}-x^{7}-x^{6}-x^{5}-x^{4}-x^{3}+x+1\,,$

for which the Mahler measure is the Salem number^[2]

${\mathcal {M}}(P(x))=1.176280818\dots \ .$

It is widely believed that this example represents the true minimal value: that is, 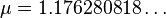$\mu =1.176280818\dots$ in Lehmer's conjecture.^[3]^[4]

Partial Results

Let $P(x)\in {\mathbb {Z}}[x]$ be an irreducible monic polynomial of degree $D$ .

Smyth ^[5] proved that Lehmer's conjecture is true for all polynomials that are not reciprocal, i.e., all polynomials satisfying 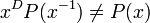$x^{D}P(x^{{-1}})\neq P(x)$ .

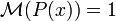Blanksby and Montgomery^[6] and Stewart^[7] independently proved that there is an absolute constant $C>1$ such that either ${\mathcal {M}}(P(x))=1$ or^[8]

$\log {\mathcal {M}}(P(x))\geq {\frac {C}{D\log D}}.$

Dobrowolski ^[9] improved this to

$\log {\mathcal {M}}(P(x))\geq C\left({\frac {\log \log D}{\log D}}\right)^{3}.$

Dobrowolski obtained the value C ≥ 1/1200 and asymptotically C > 1-ε for all sufficiently large D. Voutier obtained C ≥ 1/4 for D ≥ 2.^[10]

Elliptic Analogues

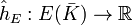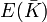Let $E/K$ be an elliptic curve defined over a number field $K$ , and let ${\hat {h}}_{E}:E({\bar {K}})\to {\mathbb {R}}$ be the canonical height function. The canonical height is the analogue for elliptic curves of the function $(\deg P)^{{-1}}\log {\mathcal {M}}(P(x))$ . It has the property that ${\hat {h}}_{E}(Q)=0$ if and only if $Q$ is a torsion point in $E({\bar {K}})$ . The elliptic Lehmer conjecture asserts that there is a constant 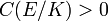$C(E/K)>0$ such that

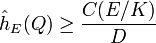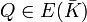${\hat {h}}_{E}(Q)\geq {\frac {C(E/K)}{D}}$ for all non-torsion points $Q\in E({\bar {K}})$ ,

where $D=[K(Q):K]$ . If the elliptic curve E has complex multiplication, then the analogue of Dobrowolski's result holds:

${\hat {h}}_{E}(Q)\geq {\frac {C(E/K)}{D}}\left({\frac {\log \log D}{\log D}}\right)^{3},$

due to Laurent.^[11] For arbitrary elliptic curves, the best known result is^[11]

${\hat {h}}_{E}(Q)\geq {\frac {C(E/K)}{D^{3}(\log D)^{2}}},$

due to Masser.^[12] For elliptic curves with non-integral j-invariant, this has been improved to^[11]

${\hat {h}}_{E}(Q)\geq {\frac {C(E/K)}{D^{2}(\log D)^{2}}},$

by Hindry and Silverman.^[13]

Restricted results

Stronger results are known for restricted classes of polynomials or algebraic numbers.

If P(x) is not reciprocal then

$M(P)\geq M(x^{3}-x-1)\approx 1.3247$

and this is clearly best possible.^[14] If further all the coefficients of P are odd then^[15]

$M(P)\geq M(x^{2}-x-1)\approx 1.618.$

If the field Q(α) is a Galois extension of Q then Lehmer's conjecture holds.^[15]

References

↑ Lehmer, D.H. (1933). "Factorization of certain cyclotomic functions". Ann. Math. (2) 34: 461–479. ISSN 0003-486X. Zbl 0007.19904.
↑ Borwein, Peter (2002). Computational Excursions in Analysis and Number Theory. CMS Books in Mathematics. Springer-Verlag. p. 16. ISBN 0-387-95444-9. Zbl 1020.12001.
↑ Smyth (2008) p.324
↑ Everest, Graham; van der Poorten, Alf; Shparlinski, Igor; Ward, Thomas (2003). Recurrence sequences. Mathematical Surveys and Monographs 104. Providence, RI: American Mathematical Society. p. 30. ISBN 0-8218-3387-1. Zbl 1033.11006.
↑ Smyth, C. J. (1971). "On the product of the conjugates outside the unit circle of an algebraic integer". Bulletin of the London Mathematical Society 3: 169–175. Zbl 1139.11002.
↑ Blanksby, P. E.; Montgomery, H. L. (1971). "Algebraic integers near the unit circle". Acta Arith. 18: 355–369. Zbl 0221.12003.
↑ Stewart, C. L. (1978). "Algebraic integers whose conjugates lie near the unit circle". Bull. Soc. Math. France 106: 169–176.
↑ Smyth (2008) p.325
↑ Dobrowolski, E. (1979). "On a question of Lehmer and the number of irreducible factors of a polynomial". Acta Arith. 34: 391–401.
↑ Smyth (2008) p.326
↑ 11.0 11.1 11.2 Smyth (2008) p.327
↑ Masser, D.W. (1989). "Counting points of small height on elliptic curves". Bull. Soc. Math. Fr. 117 (2): 247–265. Zbl 0723.14026.
↑ Hindry, Marc; Silverman, Joseph H. (1990). "On Lehmer's conjecture for elliptic curves". In Goldstein, Catherine. Sémin. Théor. Nombres, Paris/Fr. 1988-89. Prog. Math. 91. pp. 103–116. ISBN 0-8176-3493-2. Zbl 0741.14013.
↑ Smyth (2008) p.328
↑ 15.0 15.1 Smyth (2008) p.329

Smyth, Chris (2008). "The Mahler measure of algebraic numbers: a survey". In McKee, James; Smyth, Chris. Number Theory and Polynomials. London Mathematical Society Lecture Note Series 352. Cambridge University Press. pp. 322–349. ISBN 978-0-521-71467-9.

External links

http://www.cecm.sfu.ca/~mjm/Lehmer/ is a nice reference about the problem.
Weisstein, Eric W., "Lehmer's Mahler Measure Problem", MathWorld.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.