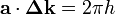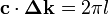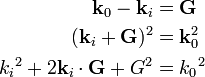Laue equations

From Wikipedia, the free encyclopedia

Laue equation

In crystallography, the Laue equations give three conditions for incident waves to be diffracted by a crystal lattice. They are named after physicist Max von Laue (1879 — 1960). They reduce to the Bragg law.

Equations

Take 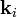${\mathbf {k}}_{i}$ to be the wavevector for the incoming (incident) beam and ${\mathbf {k}}_{o}$ to be the wavevector for the outgoing (diffracted) beam. ${\mathbf {k}}_{o}-{\mathbf {k}}_{i}={\mathbf {\Delta k}}$ is the scattering vector and measures the change between the two wavevectors.

Take 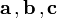${\mathbf {a}}\,,{\mathbf {b}}\,,{\mathbf {c}}$ to be the primitive vectors of the crystal lattice. The three Laue conditions for the scattering vector, or the Laue equations, for integer values of a reflection's reciprocal lattice indices (h,k,l) are as follows:

${\mathbf {a}}\cdot {\mathbf {\Delta k}}=2\pi h$

${\mathbf {b}}\cdot {\mathbf {\Delta k}}=2\pi k$

${\mathbf {c}}\cdot {\mathbf {\Delta k}}=2\pi l$

These conditions say that the scattering vector must be oriented in a specific direction in relation to the primitive vectors of the crystal lattice.

Relation to Bragg Law

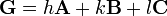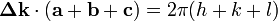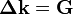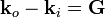If ${\mathbf {G}}=h{\mathbf {A}}+k{\mathbf {B}}+l{\mathbf {C}}$ is the reciprocal lattice vector, we know ${\mathbf {G}}\cdot ({\mathbf {a}}+{\mathbf {b}}+{\mathbf {c}})=2\pi (h+k+l)$ . The Laue equations specify ${\mathbf {\Delta k}}\cdot ({\mathbf {a}}+{\mathbf {b}}+{\mathbf {c}})=2\pi (h+k+l)$ . Hence we have ${\mathbf {\Delta k}}={\mathbf {G}}$ or ${\mathbf {k}}_{o}-{\mathbf {k}}_{i}={\mathbf {G}}$ .

From this we get the diffraction condition:

${\begin{aligned}{\mathbf {k}}_{0}-{\mathbf {k}}_{i}&={\mathbf {G}}\\({\mathbf {k}}_{i}+{\mathbf {G}})^{2}&={\mathbf {k}}_{0}^{2}\\{k_{i}}^{2}+2{\mathbf {k}}_{i}\cdot {\mathbf {G}}+G^{2}&={k_{0}}^{2}\end{aligned}}$

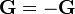Since $({\mathbf {k}}_{0})^{2}=({\mathbf {k}}_{i})^{2}$ (considering elastic scattering) and ${\mathbf {G}}=-{\mathbf {G}}$ (a negative reciprocal lattice vector is still a reciprocal lattice vector):

$2{\mathbf {k}}_{i}\cdot {\mathbf {G}}=G^{2}$ .

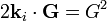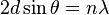The diffraction condition $\;2{\mathbf {k}}_{i}\cdot {\mathbf {G}}=G^{2}$ reduces to the Bragg law $\;2d\sin \theta =n\lambda$ .

References

Kittel, C. (1976). Introduction to Solid State Physics, New York: John Wiley & Sons. ISBN 0-471-49024-5

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.