Langlands decomposition

From Wikipedia, the free encyclopedia

In mathematics, the Langlands decomposition writes a parabolic subgroup P of a semisimple Lie group as a product 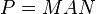$P=MAN$ of a reductive subgroup M, an abelian subgroup A, and a nilpotent subgroup N.

Applications

See also: Parabolic induction

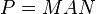A key application is in parabolic induction, which leads to the Langlands program: if $G$ is a reductive algebraic group and $P=MAN$ is the Langlands decomposition of a parabolic subgroup P, then parabolic induction consists of taking a representation of 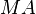$MA$ , extending it to $P$ by letting $N$ act trivially, and inducing the result from $P$ to $G$ .

See also

Lie group decompositions

References

A. W. Knapp, Structure theory of semisimple Lie groups. ISBN 0-8218-0609-2.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.