Landau distribution

From Wikipedia, the free encyclopedia

Landau distribution with mode at 2 and sigma of 1

In probability theory, the Landau distribution^[1] is a probability distribution named after Lev Landau. Because of the distribution's long tail, the moments of the distribution, like mean or variance, are undefined. The distribution is a special case of the stable distribution.

Definition

The probability density function of a standard version of the Landau distribution is defined by the complex integral

$p(x)={\frac {1}{2\pi i}}\int _{{c-i\infty }}^{{c+i\infty }}\!e^{{s\log s+xs}}\,ds,$

where c is any positive real number, and log refers to the logarithm base e, the natural logarithm. The result does not change if c changes. For numerical purposes it is more convenient to use the following equivalent form of the integral,

$p(x)={\frac {1}{\pi }}\int _{0}^{\infty }\!e^{{-t\log t-xt}}\sin(\pi t)\,dt.$

The full family of Landau distributions is obtained by extending the standard distribution to a location-scale family.

This distribution is a special case of the stable distribution with parameters α = 1, and β = 1.^[2]

The characteristic function may be expressed as:

$\varphi (t;\mu ,c)=\exp \!{\Big [}\;it\mu -|c\,t|(1+{\tfrac {2i}{\pi }}\log(|t|)){\Big ]}.$

where μ and c are real, which yields a Landau distribution shifted by μ and scaled by c.^[3]

Related distributions

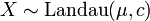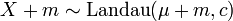
If $X\sim {\textrm {Landau}}(\mu ,c)\,$ then $X+m\sim {\textrm {Landau}}(\mu +m,c)\,$
The Landau distribution is a stable distribution

References

↑ Landau, L. (1944). "On the energy loss of fast particles by ionization". J. Phys. (USSR) 8: 201.
↑ Gentle, James E. (2003). Random Number Generation and Monte Carlo Methods. Statistics and Computing (2nd ed.). New York, NY: Springer. p. 196. doi:10.1007/b97336. ISBN 978-0-387-00178-4.
↑ Meroli, S. (2011). "Energy loss measurement for charged particles in very thin silicon layers". JINST 6: 6013.

Probability distributions

Discrete univariate with finite support

Benford Bernoulli Beta-binomial binomial categorical hypergeometric Poisson binomial Rademacher discrete uniform Zipf Zipf–Mandelbrot

Discrete univariate with infinite support

beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Gauss–Kuzmin geometric logarithmic negative binomial parabolic fractal Poisson Skellam Yule–Simon zeta

Continuous univariate supported on a bounded interval, e.g. [0,1]

Arcsine ARGUS Balding–Nichols Bates Beta Beta rectangular Irwin–Hall Kumaraswamy logit-normal Noncentral beta raised cosine Triangular U-quadratic uniform Wigner semicircle Xenakis

[[List of probability distributions#Supported_on_semi-infinite_intervals.2C_usually_.5B0.2C.E2.88.9E.29|Continuous univariate supported on a semi-infinite interval, usually [0,∞)]]

Benini
Benktander 1st kind
Benktander 2nd kind
Beta prime
Burr
chi-squared
chi
Coxian
Dagum
Davis
EL
Erlang
exponential
F
folded normal
Flory-Schulz
Fréchet
Gamma
Gamma/Gompertz
generalized inverse Gaussian
Gompertz
half-logistic
half-normal
Hotelling's T-squared
hyper-Erlang
hyperexponential
hypoexponential
inverse chi-squared (scaled inverse chi-squared)
inverse Gaussian
inverse gamma
Kolmogorov
Lévy
log-Cauchy
log-Laplace
log-logistic
log-normal
Maxwell–Boltzmann
Maxwell–Jüttner
Mittag–Leffler
Nakagami
noncentral chi-squared
Pareto
phase-type
Poly-Weibull
Rayleigh
relativistic Breit–Wigner
Rice
Rosin–Rammler
shifted Gompertz
truncated normal
type-2 Gumbel
Weibull
Wilks' lambda

Continuous univariate supported on the whole real line (−∞, ∞)

Cauchy exponential power Fisher's z generalized normal generalized hyperbolic geometric stable Gumbel Holtsmark hyperbolic secant Johnson SU Landau Laplace Linnik logistic noncentral t normal (Gaussian) normal-inverse Gaussian skew normal slash stable Student's t type-1 Gumbel variance-gamma Voigt

Continuous univariate with support whose type varies

generalized extreme value generalized Pareto Tukey lambda q-Gaussian q-exponential shifted log-logistic

Mixed continuous-discrete univariate distributions

rectified Gaussian

Multivariate (joint)

Discrete Ewens multinomial Dirichlet-multinomial negative multinomial Continuous Dirichlet Generalized Dirichlet multivariate normal Multivariate stable multivariate Student normal-scaled inverse gamma normal-gamma Matrix-valued inverse matrix gamma inverse-Wishart matrix normal matrix t matrix gamma normal-inverse-Wishart normal-Wishart Wishart

Directional

Univariate (circular) directional Circular uniform univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped Lévy Bivariate (spherical) Kent Bivariate (toroidal) bivariate von Mises Multivariate von Mises–Fisher Bingham

Degenerate and singular

Degenerate discrete degenerate Dirac delta function Singular Cantor

Families

Circular compound Poisson elliptical exponential natural exponential location-scale maximum entropy mixture Pearson Tweedie wrapped

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.