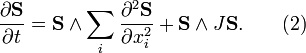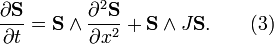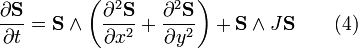Landau–Lifshitz model

From Wikipedia, the free encyclopedia
For another Landau–Lifshitz equation describing magnetism, see Landau–Lifshitz–Gilbert equation.

In solid-state physics, the Landau–Lifshitz equation (LLE), named for Lev Landau and Evgeny Lifshitz, is a partial differential equation describing time evolution of magnetism in solids, depending on 1 time variable and 1, 2, or 3 space variables.

Landau–Lifshitz equation

The LLE describes an anisotropic magnet. The equation is described in (Faddeev & Takhtajan 2007, chapter 8) as follows: It is an equation for a vector field S, in other words a function on R1+n taking values in R3. The equation depends on a fixed symmetric 3 by 3 matrix J, usually assumed to be diagonal; that is, 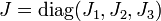J=\operatorname {diag}(J_{{1}},J_{{2}},J_{{3}}). It is given by Hamilton's equation of motion for the Hamiltonian

H={\frac {1}{2}}\int \left[\sum _{i}\left({\frac {\partial {\mathbf {S}}}{\partial x_{i}}}\right)^{{2}}-J({\mathbf {S}})\right]\,dx\qquad (1)

(where J(S) is the quadratic form of J applied to the vector S) which is

{\frac {\partial {\mathbf {S}}}{\partial t}}={\mathbf {S}}\wedge \sum _{i}{\frac {\partial ^{2}{\mathbf {S}}}{\partial x_{i}^{{2}}}}+{\mathbf {S}}\wedge J{\mathbf {S}}.\qquad (2)

In 1+1 dimensions this equation is

{\frac {\partial {\mathbf {S}}}{\partial t}}={\mathbf {S}}\wedge {\frac {\partial ^{2}{\mathbf {S}}}{\partial x^{{2}}}}+{\mathbf {S}}\wedge J{\mathbf {S}}.\qquad (3)

In 2+1 dimensions this equation takes the form

{\frac {\partial {\mathbf {S}}}{\partial t}}={\mathbf {S}}\wedge \left({\frac {\partial ^{2}{\mathbf {S}}}{\partial x^{{2}}}}+{\frac {\partial ^{2}{\mathbf {S}}}{\partial y^{{2}}}}\right)+{\mathbf {S}}\wedge J{\mathbf {S}}\qquad (4)

which is the (2+1)-dimensional LLE. For the (3+1)-dimensional case LLE looks like

{\frac {\partial {\mathbf {S}}}{\partial t}}={\mathbf {S}}\wedge \left({\frac {\partial ^{2}{\mathbf {S}}}{\partial x^{{2}}}}+{\frac {\partial ^{2}{\mathbf {S}}}{\partial y^{{2}}}}+{\frac {\partial ^{2}{\mathbf {S}}}{\partial z^{{2}}}}\right)+{\mathbf {S}}\wedge J{\mathbf {S}}.\qquad (5)

Integrable reductions

In general case LLE (2) is nonintegrable. But it admits the two integrable reductions:

a) in the 1+1 dimensions, that is Eq. (3), it is integrable
b) when 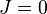J=0. In this case the (1+1)-dimensional LLE (3) turns into the continuous classical Heisenberg ferromagnet equation (see e.g. Heisenberg model (classical)) which is already integrable.

See also

References

  • Faddeev, Ludwig D.; Takhtajan, Leon A. (2007), Hamiltonian methods in the theory of solitons, Classics in Mathematics, Berlin: Springer, pp. x+592, ISBN 978-3-540-69843-2, MR 2348643 
  • Guo, Boling; Ding, Shijin (2008), Landau-Lifshitz Equations, Frontiers of Research With the Chinese Academy of Sciences, World Scientific Publishing Company, ISBN 978-981-277-875-8 
  • Kosevich A.M., Ivanov B.A., Kovalev A.S. Nonlinear magnetization waves. Dynamical and topological solitons. – Kiev: Naukova Dumka, 1988. – 192 p.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.