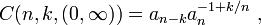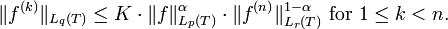Landau–Kolmogorov inequality

From Wikipedia, the free encyclopedia

In mathematics, the Landau–Kolmogorov inequality, named after Edmund Landau and Andrey Kolmogorov, is the following family of interpolation inequalities between different derivatives of a function f defined on a subset T of the real numbers:^[1]

$\|f^{{(k)}}\|_{{L_{\infty }(T)}}\leq C(n,k,T){\|f\|_{{L_{\infty }(T)}}}^{{1-k/n}}{\|f^{{(n)}}\|_{{L_{\infty }(T)}}}^{{k/n}}{\text{ for }}1\leq k<n.$

On the real line

For k = 1, n = 2, T=R the inequality was first proved by Edmund Landau^[2] with the sharp constant C(2, 1, R) = 2. Following contributions by Jacques Hadamard and Georgiy Shilov, Andrey Kolmogorov found the sharp constants and arbitrary n, k:^[3]

$C(n,k,(0,\infty ))=a_{{n-k}}a_{n}^{{-1+k/n}}~,$

where a_n are the Favard constants.

On the half-line

Following work by Matorin and others, the extremising functions were found by Isaac Jacob Schoenberg,^[4] explicit forms for the sharp constants are however still unknown.

Generalisations

There are many generalisations, which are of the form

$\|f^{{(k)}}\|_{{L_{q}(T)}}\leq K\cdot {\|f\|_{{L_{p}(T)}}^{\alpha }}\cdot {\|f^{{(n)}}\|_{{L_{r}(T)}}^{{1-\alpha }}}{\text{ for }}1\leq k<n.$

Here all three norms can be different from each other (from L₁ to L_∞, with p=q=r=∞ in the classical case) and T may be the real axis, semiaxis or a closed segment.

Notes

↑ Weisstein, E.W. "Landau-Kolmogorov Constants". MathWorld--A Wolfram Web Resource.
↑ Landau, E. (1913). "Ungleichungen für zweimal differenzierbare Funktionen". Proc. London Math. Soc. 13: 43–49.
↑ Kolmogorov, A. (1962). "On Inequalities Between the Upper Bounds of the Successive Derivatives of an Arbitrary Function on an Infinite Integral". Amer. Math. Soc. Translations. 1–2: 233–243.
↑ Schoenbergfirst=I.J. (1973). "The Elementary Case of Landau's Problem of Inequalities Between Derivatives.". Amer. Math. Monthly 80: 121–158.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.