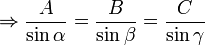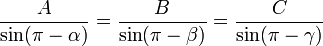Lami's theorem

From Wikipedia, the free encyclopedia

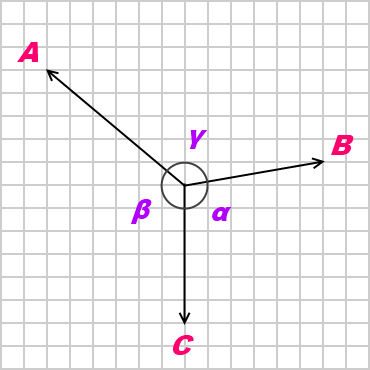
In statics, Lami's theorem is an equation relating the magnitudes of three coplanar, concurrent and non-collinear forces, which keeps an object in static equilibrium, with the angles directly opposite to the corresponding forces. A,B,C

where A, B and C are the magnitudes of three coplanar, concurrent and non-collinear forces, which keep the object in static equilibrium, and

α, β and γ are the angles directly opposite to the forces A, B and C respectively.

$\Rightarrow {\frac {A}{\sin \alpha }}={\frac {B}{\sin \beta }}={\frac {C}{\sin \gamma }}$

Lami's theorem is applied in static analysis of mechanical and structural systems. The theorem is named after Bernard Lamy.

Proof of Lami's Theorem

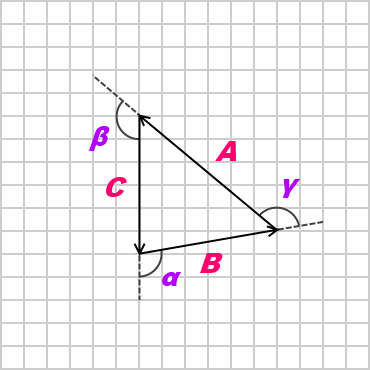
Suppose there are three coplanar, concurrent and non-collinear forces, which keeps the object in static equilibrium. By the triangle law, we can re-construct the diagram as follow:

By the law of sines,

${\frac {A}{\sin(\pi -\alpha )}}={\frac {B}{\sin(\pi -\beta )}}={\frac {C}{\sin(\pi -\gamma )}}$

$\Rightarrow {\frac {A}{\sin \alpha }}={\frac {B}{\sin \beta }}={\frac {C}{\sin \gamma }}$

Lami's theorem

Proof of Lami's Theorem

See also

Further reading