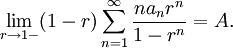Lambert summation

From Wikipedia, the free encyclopedia

In mathematical analysis, Lambert summation is a summability method for a class of divergent series.

Definition

A series $\sum a_{n}$ is Lambert summable to A, written $\sum a_{n}=A\,({\mathrm {L}})$ , if

$\lim _{{r\rightarrow 1-}}(1-r)\sum _{{n=1}}^{\infty }{\frac {na_{n}r^{n}}{1-r^{n}}}=A.\,$

If a series is convergent to A then it is Lambert summable to A (an Abelian theorem).

$\sum _{{n=1}}^{\infty }{\frac {\mu (n)}{n}}=0({\mathrm {L}})$ , where μ is the Möbius function. Hence if this series converges at all, it converges to zero.

Jacob Korevaar (2004). Tauberian theory. A century of developments. Grundlehren der Mathematischen Wissenschaften 329. Springer-Verlag. p. 18. ISBN 3-540-21058-X.
Hugh L. Montgomery; Robert C. Vaughan (2007). Multiplicative number theory I. Classical theory. Cambridge tracts in advanced mathematics 97. Cambridge: Cambridge Univ. Press. pp. 159–160. ISBN 0-521-84903-9. Cite uses deprecated parameters (help)
Norbert Wiener (1932). "Tauberian theorems". Ann. Of Math. (The Annals of Mathematics, Vol. 33, No. 1) 33 (1): 1–100. doi:10.2307/1968102. JSTOR 1968102.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.