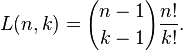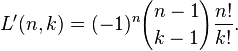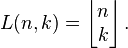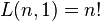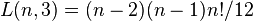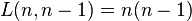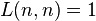Lah number

From Wikipedia, the free encyclopedia

In mathematics, Lah numbers, discovered by Ivo Lah in 1955,[1] are coefficients expressing rising factorials in terms of falling factorials.

Unsigned Lah numbers have an interesting meaning in combinatorics: they count the number of ways a set of n elements can be partitioned into k nonempty linearly ordered subsets. Lah numbers are related to Stirling numbers.

Unsigned Lah numbers:

L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}.

Signed Lah numbers:

L'(n,k)=(-1)^{n}{n-1 \choose k-1}{\frac {n!}{k!}}.

L(n, 1) is always n!; using the interpretation above, the only partition of {1, 2, 3} into 1 set can have its set ordered in 6 ways:

{(1, 2, 3)}, {(1, 3, 2)}, {(2, 1, 3)}, {(2, 3, 1)}, {(3, 1, 2)} or {(3, 2, 1)}

L(3, 2) corresponds to the 6 partitions with two ordered parts:

{(1), (2, 3)}, {(1), (3, 2)}, {(2), (1, 3)}, {(2), (3, 1)}, {(3), (1, 2)} or {(3), (2, 1)}

L(n, n) is always 1; e.g., partitioning {1, 2, 3} into 3 non-empty subsets results in subsets of length 1.

{(1), (2), (3)}

Paraphrasing Karamata-Knuth notation for Stirling numbers, it was proposed to use the following alternative notation for Lah numbers:

L(n,k)=\left\lfloor {\begin{matrix}n\\k\end{matrix}}\right\rfloor .

Rising and falling factorials

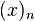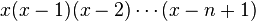Let x^{{(n)}} represent the rising factorial x(x+1)(x+2)\cdots (x+n-1) and let (x)_{n} represent the falling factorial x(x-1)(x-2)\cdots (x-n+1).

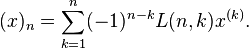
Then x^{{(n)}}=\sum _{{k=1}}^{n}L(n,k)(x)_{k} and (x)_{n}=\sum _{{k=1}}^{n}(-1)^{{n-k}}L(n,k)x^{{(k)}}.

For example, 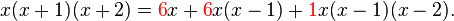x(x+1)(x+2)={\color {Red}6}x+{\color {Red}6}x(x-1)+{\color {Red}1}x(x-1)(x-2).

Compare the third row of the table of values.

Identities and relations

L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}={n \choose k}{\frac {(n-1)!}{(k-1)!}}
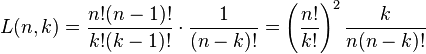
L(n,k)={\frac {n!(n-1)!}{k!(k-1)!}}\cdot {\frac {1}{(n-k)!}}=\left({\frac {n!}{k!}}\right)^{2}{\frac {k}{n(n-k)!}}
L(n,k+1)={\frac {n-k}{k(k+1)}}L(n,k).
L(n,k)=\sum _{{j}}\left[{n \atop j}\right]\left\{{j \atop k}\right\}, with \left[{n \atop j}\right] the Stirling numbers of the first kind, \left\{{j \atop k}\right\} the Stirling numbers of the second kind and with the conventions L(0,0)=1 and L(n,k)=0 if k>n.
L(n,1)=n!
L(n,2)=(n-1)n!/2
L(n,3)=(n-2)(n-1)n!/12
L(n,n-1)=n(n-1)
L(n,n)=1

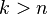Table of values

Below is a table of values for the Lah numbers:

_{n}\!\!\diagdown \!\!^{k} 1 2 3 4 5 6 7 8 9 10 11 12
1 1
2 2 1
3 6 6 1
4 24 36 12 1
5 120 240 120 20 1
6 720 1800 1200 300 30 1
7 5040 15120 12600 4200 630 42 1
8 40320 141120 141120 58800 11760 1176 56 1
9 362880 1451520 1693440 846720 211680 28224 2016 72 1
10 3628800 16329600 21772800 12700800 3810240 635040 60480 3240 90 1
11 39916800 199584000 299376000 199584000 69854400 13970880 1663200 11880 4950 110 1
12 479001600 2634508800 4390848000 3293136000 1317254400 307359360 43908480 3920400 217800 7260 132 1

See also

References

  1. ↑ Introduction to Combinatorial Analysis Princeton University Press (1958, reissue 1980) ISBN 978-0-691-02365-6 (reprinted again in 2002, by Courier Dover Publications).
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.