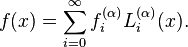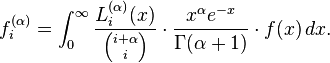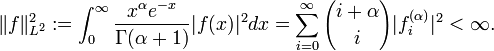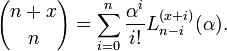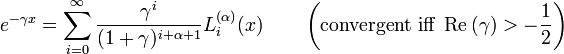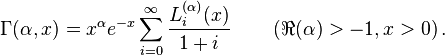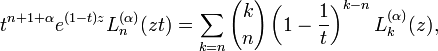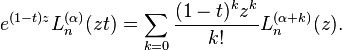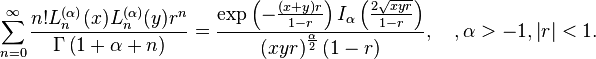Laguerre polynomials
In mathematics, the Laguerre polynomials, named after Edmond Laguerre (1834 – 1886), are solutions of Laguerre's equation:
which is a second-order linear differential equation. This equation has nonsingular solutions only if n is a non-negative integer.
The associated Laguerre polynomials (alternatively, but rarely, named Sonin polynomials, after their inventor[1] N. Y. Sonin) are solutions of
The Laguerre polynomials are also used for Gaussian quadrature to numerically compute integrals of the form
These polynomials, usually denoted L0, L1, ..., are a polynomial sequence which may be defined by the Rodrigues formula,
reducing to the closed form of a following section.
They are orthogonal polynomials with respect to an inner product
The sequence of Laguerre polynomials n! Ln is a Sheffer sequence, d⁄dx Ln = (d⁄dx−1) Ln−1.
The Rook polynomials in combinatorics are more or less the same as Laguerre polynomials, up to elementary changes of variables.
The Laguerre polynomials arise in quantum mechanics, in the radial part of the solution of the Schrödinger equation for a one-electron atom. They also describe the static Wigner functions of oscillator systems in quantum mechanics in phase space. They further enter in the quantum mechanics of the 3D isotropic harmonic oscillator.
Physicists sometimes use a definition for the Laguerre polynomials which is larger by a factor of n! than the definition used here. (Likewise, some physicist may use somewhat different definitions of the so-called associated Laguerre polynomials.)
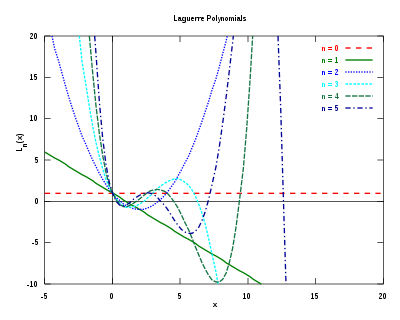
The first few polynomials
These are the first few Laguerre polynomials:
| n | 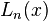 |
| 0 |  |
| 1 | 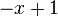 |
| 2 |  |
| 3 | 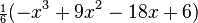 |
| 4 | 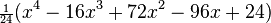 |
| 5 | 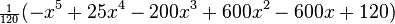 |
| 6 |  |
Recursive definition, closed form, and generating function
One can also define the Laguerre polynomials recursively, defining the first two polynomials as
and then using the following recurrence relation for any k ≥ 1:
The closed form is
The generating function for them likewise follows,
Generalized Laguerre polynomials
For arbitrary real α the polynomial solutions of the differential equation [2]
are called generalized Laguerre polynomials, or associated Laguerre polynomials.
The simple Laguerre polynomials are included in the associated polynomials, through α = 0,
The Rodrigues formula for them is
The generating function for them is
Explicit examples and properties of the associated Laguerre polynomials
- Laguerre functions are defined by confluent hypergeometric functions and Kummer's transformation as[3]
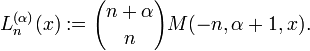
- When n is an integer the function reduces to a polynomial of degree n. It has the alternative expression[4]
-
- in terms of Kummer's function of the second kind.
- The closed form for these associated Laguerre polynomials of degree n is[5]
-
- derived by applying Leibniz's theorem for differentiation of a product to Rodrigues' formula.
- The first few generalized Laguerre polynomials are:
| n |  |
| 0 |  |
| 1 |  |
| 2 | 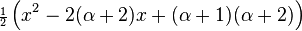 |
| 3 | 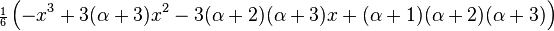 |
- The coefficient of the leading term is (−1)n/n!;
- The constant term, which is the value at 0, is
- Ln(α) has n real, strictly positive roots (notice that
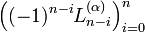 is a Sturm chain), which are all in the interval
is a Sturm chain), which are all in the interval ![\left(0,n+\alpha +(n-1){\sqrt {n+\alpha }}\right].](/2014-wikipedia_en_all_02_2014/I/media/7/9/c/6/79c6a04a69201eebd6efed4a80b78703.png) [citation needed]
[citation needed]
-
- and summarizing by
-
- where
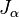 is the Bessel function.
is the Bessel function.
- Moreover[citation needed]
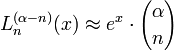 ,
,
- whenever n tends to infinity.
As a contour integral
Given the generating function specified above, the polynomials may be expressed in terms of a contour integral
where the contour circles the origin once in a counterclockwise direction.
Recurrence relations
The addition formula for Laguerre polynomials:[8]
-
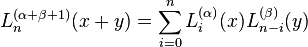 .
.
Laguerre's polynomials satisfy the recurrence relations
in particular
and
or
moreover
They can be used to derive the four 3-point-rules
combined they give this additional, useful recurrence relations
A somewhat curious identity, valid for integer i and n, is
it may be used to derive the partial fraction decomposition
Derivatives of generalized Laguerre polynomials
Differentiating the power series representation of a generalized Laguerre polynomial k times leads to
This points to a special case (α = 0) of the formula above:
for integer α = k the generalized polynomial may be written
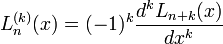 , the shift by k sometimes causing confusion with the usual parenthesis notation for a
derivative.
, the shift by k sometimes causing confusion with the usual parenthesis notation for a
derivative.
Moreover, this following equation holds
which generalizes with Cauchy's formula to
The derivative with respect to the second variable α has the form, [9]
This is evident from the contour integral representation below.
The generalized associated Laguerre polynomials obey the differential equation
which may be compared with the equation obeyed by the kth derivative of the ordinary Laguerre polynomial,
where 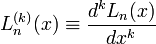 for this equation only.
for this equation only.
In Sturm–Liouville form the differential equation is
which shows that Lα
n is an eigenvector for the eigenvalue n.
Orthogonality
The associated Laguerre polynomials are orthogonal over [0, ∞) with respect to the measure with weighting function xα e −x:[10]
which follows from
If 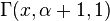 denoted the Gamma distribution then the orthogonality relation can be written as
denoted the Gamma distribution then the orthogonality relation can be written as
The associated, symmetric kernel polynomial has the representations (Christoffel–Darboux formula)[citation needed]
recursively
Moreover,
in the associated L2[0, ∞)-space.
Turán's inequalities can be derived here, which is
The following integral is needed in the quantum mechanical treatment of the hydrogen atom,
Series expansions
Let a function have the (formal) series expansion
Then
The series converges in the associated Hilbert space 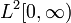 , iff
, iff
Further examples of expansions
Monomials are represented as
while binomials have the parametrization
This leads directly to
for the exponential function. The incomplete gamma function has the representation
Multiplication theorems
Erdélyi gives the following two multiplication theorems [11]
Relation to Hermite polynomials
The generalized Laguerre polynomials are related to the Hermite polynomials:
and
where the Hn(x) are the Hermite polynomials based on the weighting function exp(−x2), the so-called "physicist's version."
Because of this, the generalized Laguerre polynomials arise in the treatment of the quantum harmonic oscillator.
Relation to hypergeometric functions
The Laguerre polynomials may be defined in terms of hypergeometric functions, specifically the confluent hypergeometric functions, as
where  is the Pochhammer symbol (which in this case represents the rising factorial).
is the Pochhammer symbol (which in this case represents the rising factorial).
Poisson Kernel
Notes
- ↑ Sonine, N. Y. (1880): "Recherches sur les fonctions cylindriques et le développement des fonctions continues en séries", Math Ann. 16 (1880) 1.
- ↑ A&S p. 781
- ↑ A&S p.509
- ↑ A&S p.510
- ↑ A&S p. 775
- ↑ G. Szegő, "Orthogonal polynomials", 4th edition, Amer. Math. Soc. Colloq. Publ., vol. 23, Amer. Math. Soc., Providence, RI, 1975, p. 198.
- ↑ D. Borwein, J. M. Borwein, R. E. Crandall, "Effective Laguerre asymptotics", SIAM J. Numer. Anal., vol. 46 (2008), no. 6, pp. 3285-3312, http://dx.doi.org/10.1137/07068031X
- ↑ A&S equation (22.12.6), p. 785
- ↑ W. Koepf, "Identities for families of orthogonal polynomials and special functions.", Integral Transforms and Special Functions 5, (1997) pp.69-102. (Theorem 10)
- ↑ A&S p. 774
- ↑ C. Truesdell, "On the Addition and Multiplication Theorems for the Special Functions", Proceedings of the National Academy of Sciences, Mathematics, (1950) pp.752-757.
References
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 22", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, p. 773, ISBN 978-0486612720, MR 0167642.
- Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Orthogonal Polynomials", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
- B. Spain, M.G. Smith, Functions of mathematical physics, Van Nostrand Reinhold Company, London, 1970. Chapter 10 deals with Laguerre polynomials.
- Hazewinkel, Michiel, ed. (2001), "Laguerre polynomials", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Eric W. Weisstein, "Laguerre Polynomial", From MathWorld—A Wolfram Web Resource.
- George Arfken and Hans Weber (2000). Mathematical Methods for Physicists. Academic Press. ISBN 0-12-059825-6.
- S. S. Bayin (2006), Mathematical Methods in Science and Engineering, Wiley, Chapter 3.
External links
- Timothy Jones. "The Legendre and Laguerre Polynomials and the elementary quantum mechanical model of the Hydrogen Atom".
- Weisstein, Eric W., "Laguerre polynomial", MathWorld.

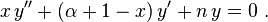

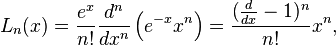
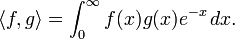
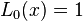
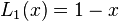
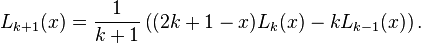
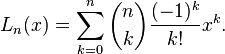
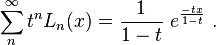
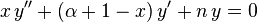
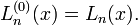
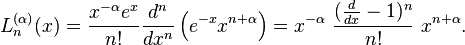
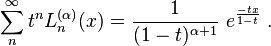


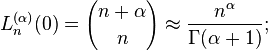

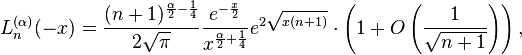



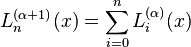
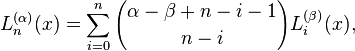
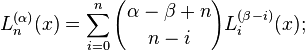
![{\begin{aligned}L_{n}^{{(\alpha )}}(x)-\sum _{{j=0}}^{{\Delta -1}}{n+\alpha \choose n-j}(-1)^{j}{\frac {x^{j}}{j!}}&=(-1)^{\Delta }{\frac {x^{\Delta }}{(\Delta -1)!}}\sum _{{i=0}}^{{n-\Delta }}{\frac {{n+\alpha \choose n-\Delta -i}}{(n-i){n \choose i}}}L_{i}^{{(\alpha +\Delta )}}(x)\\[6pt]&=(-1)^{\Delta }{\frac {x^{\Delta }}{(\Delta -1)!}}\sum _{{i=0}}^{{n-\Delta }}{\frac {{n+\alpha -i-1 \choose n-\Delta -i}}{(n-i){n \choose i}}}L_{i}^{{(n+\alpha +\Delta -i)}}(x).\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/d/8/b/a/d8ba5d3b9e8aecb5357b6329dae10c34.png)
![{\begin{aligned}L_{n}^{{(\alpha )}}(x)&=L_{n}^{{(\alpha +1)}}(x)-L_{{n-1}}^{{(\alpha +1)}}(x)=\sum _{{j=0}}^{k}{k \choose j}L_{{n-j}}^{{(\alpha -k+j)}}(x),\\[10pt]nL_{n}^{{(\alpha )}}(x)&=(n+\alpha )L_{{n-1}}^{{(\alpha )}}(x)-xL_{{n-1}}^{{(\alpha +1)}}(x),\\[10pt]&{\text{or }}{\frac {x^{k}}{k!}}L_{n}^{{(\alpha )}}(x)=\sum _{{i=0}}^{k}(-1)^{i}{n+i \choose i}{n+\alpha \choose k-i}L_{{n+i}}^{{(\alpha -k)}}(x),\\[10pt]nL_{n}^{{(\alpha +1)}}(x)&=(n-x)L_{{n-1}}^{{(\alpha +1)}}(x)+(n+\alpha )L_{{n-1}}^{{(\alpha )}}(x)\\[10pt]xL_{n}^{{(\alpha +1)}}(x)&=(n+\alpha )L_{{n-1}}^{{(\alpha )}}(x)-(n-x)L_{n}^{{(\alpha )}}(x);\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/5/8/7/8/58781bec346a1073761ddde55f0ca531.png)
![{\begin{aligned}L_{n}^{{(\alpha )}}(x)&=\left(2+{\frac {\alpha -1-x}n}\right)L_{{n-1}}^{{(\alpha )}}(x)-\left(1+{\frac {\alpha -1}n}\right)L_{{n-2}}^{{(\alpha )}}(x)\\[10pt]&={\frac {\alpha +1-x}n}L_{{n-1}}^{{(\alpha +1)}}(x)-{\frac xn}L_{{n-2}}^{{(\alpha +2)}}(x).\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/b/0/c/5/b0c5ce0e0358c6c75a7a605925297c4f.png)


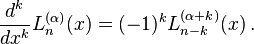
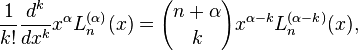


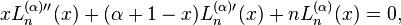



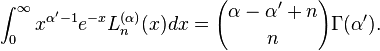
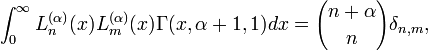
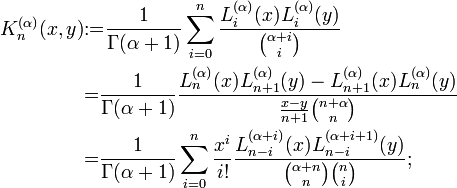
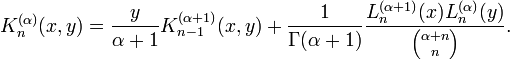
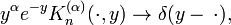
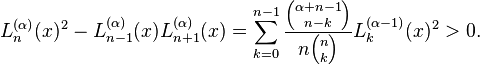
![\int _{0}^{{\infty }}x^{{\alpha +1}}e^{{-x}}\left[L_{n}^{{(\alpha )}}(x)\right]^{2}dx={\frac {(n+\alpha )!}{n!}}(2n+\alpha +1).](/2014-wikipedia_en_all_02_2014/I/media/b/1/a/9/b1a962d944b6f3ace499dc3703602b66.png)