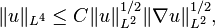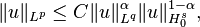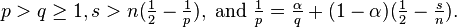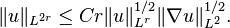Ladyzhenskaya's inequality
In mathematics, Ladyzhenskaya's inequality is any of a number of related functional inequalities named after the Soviet Russian mathematician Olga Aleksandrovna Ladyzhenskaya. The original such inequality, for functions of two real variables, was introduced by Ladyzhenskaya in 1958 to prove the existence and uniqueness of long-time solutions to the Navier–Stokes equations in two spatial dimensions (for smooth enough initial data). There is an analogous inequality for functions of three real variables, but the exponents are slightly different; much of the difficulty in establishing existence and uniqueness of solutions to the three-dimensional Navier–Stokes equations stems from these different exponents. Ladyzhenskaya's inequality is one member of a broad class of inequalities known as interpolation inequalities.
Let Ω be a Lipschitz domain in Rn for n = 2 or 3, and let u: Ω → R be a weakly differentiable function that vanishes on the boundary of Ω in the sense of trace (that is, u is a limit in the Sobolev space H1(Ω) of a sequence of smooth functions that are compactly supported in Ω). Then there exists a constant C depending only on Ω such that, in the case n = 2,
and, in the case n = 3,
Generalizations
- Both the two- and three-dimensional versions of Ladyzhenskaya's inequality are special cases of the Gagliardo–Nirenberg interpolation inequality
- which holds whenever
- Ladyzhensakaya's inequalities are the special cases p = 4, q = 2, s = 1, and α = ½ when n = 2 and α = ¼ when n = 3.
- A simple modification of the argument used by Ladyzhenskaya in her 1958 paper (see e.g. Constantin & Seregin 2010) yields the following inequality for u: R2 → R, valid for all r ≥ 2:
- The usual Ladyzhenskaya inequality on Rn, n = 2 or 3, can be generalized (see McCormick & al. 2013) to use the weak L2 “norm” of u in place of the usual L2 norm:
See also
References
- Constantin, P.; Seregin, G. (2010), "Hölder continuity of solutions of 2D Navier–Stokes equations with singular forcing", Nonlinear partial differential equations and related topics, Amer. Math. Soc. Transl. Ser. 2 229, Providence, RI: Amer. Math. Soc., pp. 87–95
- Ладыженская, О. А. (1958). "Решение "в целом" краевой задачи для уравнений Навье – Стокса в случае двух пространственных переменных". Доклады Академии наук СССР 123 (3): 427–429. [Ladyzhensakya, O. A. (1958). "Global solvability of a boundary value problem for the Navier–Stokes equations in the case of two spatial variables". Proceedings of the Academy of Sciences of the USSR 123 (3): 427–429.]
- McCormick, D. S.; Robinson, J. C.; Rodrigo, J. L. (2013). "Generalised Gagliardo–Nirenberg inequalities using weak Lebesgue spaces and BMO". Milan J. Math. doi:10.1007/s00032-013-0202-6.