LF-space

From Wikipedia, the free encyclopedia

In mathematics, an LF-space is a topological vector space V that is a locally convex inductive limit of a countable inductive system 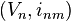$(V_{n},i_{{nm}})$ of Fréchet spaces. This means that V is a direct limit of the system 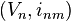$(V_{n},i_{{nm}})$ in the category of locally convex topological vector spaces and each $V_{n}$ is a Fréchet space.

Original definition was also assuming that V is a strict locally convex inductive limit, which means that the topology induced on $V_{n}$ by $V_{{n+1}}$ is identical to the original topology on $V_{n}$ .

The topology on V can be described by specifying that an absolutely convex subset U is a neighborhood of 0 if and only if $U\cap V_{n}$ is an absolutely convex neighborhood of 0 in $V_{n}$ for every n.

Properties

An LF space is complete, barrelled and bornological (and thus ultrabornological).

Examples

A typical example of an LF-space is, 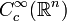$C_{c}^{\infty }({\mathbb {R}}^{n})$ , the space of all infinitely differentiable functions on ${\mathbb {R}}^{n}$ with compact support. The LF-space structure is obtained by considering a sequence of compact sets $K_{1}\subset K_{2}\subset \ldots \subset K_{i}\subset \ldots \subset {\mathbb {R}}^{n}$ with $\bigcup _{i}K_{i}={\mathbb {R}}^{n}$ and for all i, $K_{i}$ is a subset of the interior of $K_{{i+1}}$ . Such a sequence could be the balls of radius i centered at the origin. 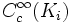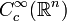The space $C_{c}^{\infty }(K_{i})$ of infinitely differentiable functions on ${\mathbb {R}}^{n}$ with compact support contained in $K_{i}$ has a natural Fréchet space structure and $C_{c}^{\infty }({\mathbb {R}}^{n})$ inherits its LF-space structure as described above. The LF-space topology does not depend on the particular sequence of compact sets $K_{i}$ .

With this LF-space structure, 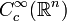$C_{c}^{\infty }({\mathbb {R}}^{n})$ is known as the space of test functions, of fundamental importance in the theory of distributions.

References

Treves, François (1967), Topological Vector Spaces, Distributions and Kernels, Academic Press, pp. p. 126 ff .

v t e Functional analysis

Local Notions on Sets	Absolutely convex Absorbing Balanced Bounded Cones (Linear, Convex cone) Convex Radial Star-shaped Symmetric

Types of TVSs	Banach Barrelled Bornological Brauner F-space Finite-dimensional Fréchet (Tame) Hilbert LF Locally convex Mackey Montel Nuclear Normed (Norm) Reflexive Riesz Smith Stereotype Topological tensor product (of Hilbert spaces) Webbed

Spaces of Maps	Dual space Dual topology Operator topologies Strong Topology (Polar, Operator) Topology of uniform convergence Weak topology (operator) Ultrastrong topology Ultraweak topology

Types of Linear operators	Adjoint Bilinear (form) Bounded (Unbounded) Closed Continuous (Discontinuous) Compact Fredholm Hilbert–Schmidt Functionals (Positive) Normal Nuclear Self-adjoint Strictly singular Trace class Transpose Unitary

Operations on Sets	Algebraic interior (core) Interior Minkowski addition Polar

Banach Algebras	C-algebras Spectrum (of a C-algebra, Spectral radius) Spectral theory

Important Theorems	Banach–Alaoglu Banach–Saks Banach–Mazur Bessel's inequality Cauchy–Schwarz inequality Closed range Closed graph Eberlein–Šmulian Freudenthal spectral Gelfand–Mazur Goldstine Hahn–Banach (Hyperplane separation) Kakutani fixed-point Lomonosov's Invariant Subspace Mackey–Arens Mazur's lemma M. Riesz extension Open mapping Parseval's identity Schauder fixed-point

Analysis	Bochner space Derivatives (Fréchet derivative, Gâteaux derivative, Functional, Holomorphy) Differentiation in Fréchet spaces Integrals (Bochner, Dunford, Gelfand–Pettis, Regulated, Weak) Functional calculus Inverse function theorem (Nash–Moser theorem) Vector measure

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.