Lüroth's theorem
In mathematics, Lüroth's theorem, named after Jacob Lüroth, is a result of field theory, which is related to rational varieties. It asserts that every field extension of a field  , which is also a subfield of
, which is also a subfield of  , is simple.
, is simple.
Statement of the theorem
Let  be a field and
be a field and  be an intermediate field between
be an intermediate field between  and
and  , for some indeterminate X. Then there exists a rational function
, for some indeterminate X. Then there exists a rational function  such that
such that 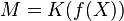 . In other words, every
intermediate extension between
. In other words, every
intermediate extension between  and
and  is simple.
is simple.
The proof of Lüroth's theorem can be derived easily from the theory of rational curves, using the geometrical notion of genus. Even though Lüroth's theorem is generally thought to be non elementary, several short proofs, using only the basics of field theory, have been discovered for long. Virtually all these simple proofs use Gauss's lemma on primitive polynomials as a main step (see e.g. [1]).
See also
- Rational variety
- Rational curve
- Rational surface
- Birational geometry
References
- ↑ Bensimhoun, Michael (May 2004). 's_theorem-06.2004.pdf Another elementary proof of Lüroth's theorem (PDF).
- Burau, Werner (2008), "Lueroth (or Lüroth), Jakob", Complete Dictionary of Scientific Biography