Kurepa tree
From Wikipedia, the free encyclopedia
In set theory, a Kurepa tree is a tree (T, <) of height 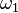 , each of whose levels is at most countable, and has at least
, each of whose levels is at most countable, and has at least 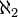 many branches. It was named after Yugoslav mathematician Đuro Kurepa. The existence of a Kurepa tree (known as the Kurepa hypothesis) is consistent with the axioms of ZFC: As Solovay showed, there are Kurepa trees in Gödel's constructible universe. On the other hand, as Silver proved in 1971, if a strongly inaccessible cardinal is Lévy collapsed to
many branches. It was named after Yugoslav mathematician Đuro Kurepa. The existence of a Kurepa tree (known as the Kurepa hypothesis) is consistent with the axioms of ZFC: As Solovay showed, there are Kurepa trees in Gödel's constructible universe. On the other hand, as Silver proved in 1971, if a strongly inaccessible cardinal is Lévy collapsed to  then, in the resulting model, there are no Kurepa trees.
then, in the resulting model, there are no Kurepa trees.
See also
References
- Jech, Thomas (2002). Set Theory. Springer-Verlag. ISBN 3-540-44085-2.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.