Kuratowski closure axioms

From Wikipedia, the free encyclopedia

In topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition. They were first introduced by Kazimierz Kuratowski, in a slightly different form that applied only to Hausdorff spaces.

A similar set of axioms can be used to define a topological structure using only the dual notion of interior operator.

Definition

Let $X$ be a set and ${\mathcal {P}}(X)$ its power set.
A Kuratowski Closure Operator is an assignment 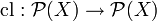$\operatorname {cl}:{\mathcal {P}}(X)\to {\mathcal {P}}(X)$ with the following properties:

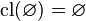$\operatorname {cl}(\varnothing )=\varnothing$ (Preservation of Nullary Union)
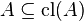$A\subseteq \operatorname {cl}(A)$ (Extensivity)
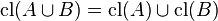$\operatorname {cl}(A\cup B)=\operatorname {cl}(A)\cup \operatorname {cl}(B)$ (Preservation of Binary Union)
$\operatorname {cl}(\operatorname {cl}(A))=\operatorname {cl}(A)\!$ (Idempotence)

If the last axiom, Idempotence, is omitted, then the axioms define a Preclosure Operator.
A consequence from the third axiom is: $A\subseteq B\Rightarrow \operatorname {cl}(A)\subseteq \operatorname {cl}(B)$ (Preservation of Inclusion)

Connection to other Axiomatizations of Topology

Induction of Topology

Construction
A closure operator naturally induces a topology as follows:
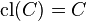A subset $C\subseteq X$ is called closed if and only if $\operatorname {cl}(C)=C$ .

Empty Set and Entire Space are closed:
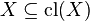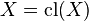By Extensitivity $X\subseteq \operatorname {cl}(X)$ and since Closure maps into itself $\operatorname {cl}(X)\subseteq X$ we have $X=\operatorname {cl}(X)$ . Thus $X$ is closed.
By Preservation of Nullary Unions follows 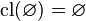$\operatorname {cl}(\varnothing )=\varnothing$ . Thus 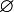$\varnothing$ is closed

Arbitrary intersections of closed sets is closed:
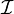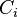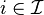Let ${\mathcal {I}}$ be an arbitrary set of indices and $C_{i}$ closed for every $i\in {\mathcal {I}}$ .
Then by Extensitivity: 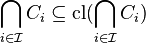$\bigcap _{{i\in {\mathcal {I}}}}C_{i}\subseteq \operatorname {cl}(\bigcap _{{i\in {\mathcal {I}}}}C_{i})$
Also by Preservation of Inclusions: $\bigcap _{{i\in {\mathcal {I}}}}C_{i}\subseteq C_{i}\forall i\in {\mathcal {I}}\Rightarrow \operatorname {cl}(\bigcap _{{i\in {\mathcal {I}}}}C_{i})\subseteq \operatorname {cl}(C_{i})=C_{i}\forall i\in {\mathcal {I}}\Rightarrow \operatorname {cl}(\bigcap _{{i\in {\mathcal {I}}}}C_{i})\subseteq \bigcap _{{i\in {\mathcal {I}}}}C_{i}$
And therefore 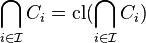$\bigcap _{{i\in {\mathcal {I}}}}C_{i}=\operatorname {cl}(\bigcap _{{i\in {\mathcal {I}}}}C_{i})$ . Thus 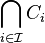$\bigcap _{{i\in {\mathcal {I}}}}C_{i}$ is closed.

Finite unions of closed sets is closed:
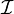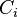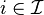Let ${\mathcal {I}}$ be a finite set of indices and $C_{i}$ closed for every $i\in {\mathcal {I}}$ .
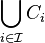From the Preservation of binary unions and by induction we have $\bigcup _{{i\in {\mathcal {I}}}}C_{i}=\operatorname {cl}(\bigcup _{{i\in {\mathcal {I}}}}C_{i})$ . Thus $\bigcup _{{i\in {\mathcal {I}}}}C_{i}$ is closed.

Induction of Closure

The induced topology reinduces a closure which agrees with the original closure: 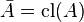${\bar {A}}=\operatorname {cl}(A)$
For a proof see Alternative Characterizations of Topological Spaces.

Recovering Notions from Topology

Closeness
A point $p$ is close to a subset $A$ iff $p\in \operatorname {cl}(A)$ .

Continuity
A function $f:X\to Y$ is continuous at a point $p$ iff $p\in \operatorname {cl}(A)\Rightarrow f(p)\in \operatorname {cl}(f(A))$ .

External links

Alternative Characterizations of Topological Spaces

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.