Krull ring

From Wikipedia, the free encyclopedia

In commutative algebra, a Krull ring or Krull domain is a commutative ring with a well behaved theory of prime factorization. They were introduced by Wolfgang Krull (1931). They are a higher-dimensional generalization of Dedekind domains, which are exactly the Krull domains of dimension at most 1.

In this article, a ring is commutative and has unity.

Formal definition

Let $A$ be an integral domain and let $P$ be the set of all prime ideals of $A$ of height one, that is, the set of all prime ideals properly containing no nonzero prime ideal. Then $A$ is a Krull ring if and only if

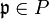$A_{{{\mathfrak {p}}}}$ is a discrete valuation ring for all ${\mathfrak {p}}\in P$ ,
$A$ is the intersection of these discrete valuation rings (considered as subrings of the quotient field of $A$ ).
Any nonzero element of $A$ is contained in only a finite number of height 1 prime ideals.

Properties

A Krull domain is a unique factorization domain if and only if every prime ideal of height one is principal.^[1]

Let A be a Zariski ring (e.g., a local noetherian ring). If the completion $\widehat {A}$ is a Krull domain, then A is a Krull domain.^[2]

Examples

Every integrally closed noetherian domain is a Krull ring. In particular, Dedekind domains are Krull rings. Conversely Krull rings are integrally closed, so a Noetherian domain is Krull if and only if it is integrally closed.
If $A$ is a Krull ring then so is the polynomial ring $A[x]$ and the formal power series ring $A[[x]]$ .
The polynomial ring $R[x_{1},x_{2},x_{3},\ldots ]$ in infinitely many variables over a unique factorization domain $R$ is a Krull ring which is not noetherian. In general, any unique factorization domain is a Krull ring.
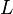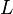Let $A$ be a Noetherian domain with quotient field $K$ , and $L$ be a finite algebraic extension of $K$ . Then the integral closure of $A$ in $L$ is a Krull ring (Mori–Nagata theorem).^[3]

The divisor class group of a Krull ring

A (Weil) divisor of a Krull ring A is a formal integral linear combination of the height 1 prime ideals, and these form a group D(A). A divisor of the form div(x) for some non-zero x in A is called a principal divisor, and the principal divisors form a subgroup of the group of divisors. The quotient of the group of divisors by the subgroup of principal divisors is called the divisor class group of A.

A Cartier divisor of a Krull ring is a locally principal (Weil) divisor. The Cartier divisors form a subgroup of the group of divisors containing the principal divisors. The quotient of the Cartier divisors by the principal divisors is a subgroup of the divisor class group, isomorphic to the Picard group of invertible sheaves on Spec(A).

Example: in the ring k[x,y,z]/(xy–z²] the divisor class group has order 2, generated by the divisor y=z, but the Picard subgroup is the trivial group.

References

↑ http://eom.springer.de/k/k055930.htm
↑ Bourbaki, 7.1, no 10, Proposition 16.
↑ http://books.google.com/books?id=APPtnn84FMIC&lpg=PA83&ots=2L9MiWbIYZ&dq=krull%20akizuki&pg=PA85#v=onepage&q=krull%20akizuki&f=false

N. Bourbaki. Commutative algebra.
Hazewinkel, Michiel, ed. (2001), "Krull ring", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Krull, Wolfgang (1931), "Allgemeine Bewertungstheorie", J. Reine Angew. Math. 167: 160–196
Hideyuki Matsumura, Commutative Algebra. Second Edition. Mathematics Lecture Note Series, 56. Benjamin/Cummings Publishing Co., Inc., Reading, Mass., 1980. xv+313 pp. ISBN 0-8053-7026-9
Hideyuki Matsumura, Commutative Ring Theory. Translated from the Japanese by M. Reid. Cambridge Studies in Advanced Mathematics, 8. Cambridge University Press, Cambridge, 1986. xiv+320 pp. ISBN 0-521-25916-9
Samuel, Pierre (1964), Murthy, M. Pavman, ed., Lectures on unique factorization domains, Tata Institute of Fundamental Research Lectures on Mathematics 30, Bombay: Tata Institute of Fundamental Research, MR 0214579

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.