Koszul complex

From Wikipedia, the free encyclopedia

In mathematics, the Koszul complex was first introduced to define a cohomology theory for Lie algebras, by Jean-Louis Koszul (see Lie algebra cohomology). It turned out to be a useful general construction in homological algebra.

Introduction

In commutative algebra, if x is an element of the ring R, multiplication by x is R-linear and so represents an R-module homomorphism x:R →R from R to itself. It is useful to throw in zeroes on each end and make this a (free) R-complex:

$0\to R{\xrightarrow {\ x\ }}R\to 0.$

Call this chain complex K_•(x).

Counting the right-hand copy of R as the zeroth degree and the left-hand copy as the first degree, this chain complex neatly captures the most important facts about multiplication by x because its zeroth homology is exactly the homomorphic image of R modulo the multiples of x, H₀(K_•(x)) = R/xR, and its first homology is exactly the annihilator of x, H₁(K_•(x)) = Ann_R(x).

This chain complex K_•(x) is called the Koszul complex of R with respect to x.

Now, if x₁, x₂, ..., x_n are elements of R, the Koszul complex of R with respect to x₁, x₂, ..., x_n, usually denoted K_•(x₁, x₂, ..., x_n), is the tensor product in the category of R-complexes of the Koszul complexes defined above individually for each i.

The Koszul complex is a free chain complex. There are exactly (n choose j) copies of the ring R in the jth degree in the complex (0 ≤ j ≤ n). The matrices involved in the maps can be written down precisely. Letting $e_{{i_{1}...i_{p}}}$ denote a free-basis generator in K_p, d: K_p ↦ K_{p − 1} is defined by:

$d(e_{{i_{1}...i_{p}}}):=\sum _{{j=1}}^{{p}}(-1)^{{j-1}}x_{{i_{j}}}e_{{i_{1}...\widehat {i_{j}}...i_{p}}}.$

For the case of two elements x and y, the Koszul complex can then be written down quite succinctly as

$0\to R{\xrightarrow {\ d_{2}\ }}R^{2}{\xrightarrow {\ d_{1}\ }}R\to 0,$

with the matrices 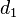$d_{1}$ and $d_{2}$ given by

$d_{1}={\begin{bmatrix}x&y\\\end{bmatrix}}$ and

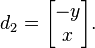
$d_{2}={\begin{bmatrix}-y\\x\\\end{bmatrix}}.$

Note that d_i is applied on the left. The cycles in degree 1 are then exactly the linear relations on the elements x and y, while the boundaries are the trivial relations. The first Koszul homology H₁(K_•(x, y)) therefore measures exactly the relations mod the trivial relations. With more elements the higher-dimensional Koszul homologies measure the higher-level versions of this.

In the case that the elements x₁, x₂, ..., x_n form a regular sequence, the higher homology modules of the Koszul complex are all zero.

Example

If k is a field and X₁, X₂, ..., X_d are indeterminates and R is the polynomial ring k[X₁, X₂, ..., X_d], the Koszul complex K_•(X_i) on the X_i's forms a concrete free R-resolution of k.

Theorem

Let (R, m) be a Noetherian local ring with maximal ideal m, and let M be a finitely-generated R-module. If x₁, x₂, ..., x_n are elements of the maximal ideal m, then the following are equivalent:

The (x_i) form a regular sequence on M,
H₁(K_•(x_i)) = 0,
H_j(K_•(x_i)) = 0 for all j ≥ 1.

Applications

The Koszul complex is essential in defining the joint spectrum of a tuple of bounded linear operators in a Banach space.

References

David Eisenbud, Commutative Algebra. With a view toward algebraic geometry, Graduate Texts in Mathematics, vol 150, Springer-Verlag, New York, 1995. ISBN 0-387-94268-8

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.