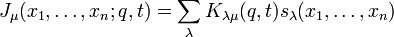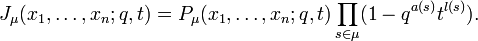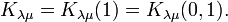Kostka polynomial
In mathematics, Kostka polynomials, named after the mathematician Carl Kostka, are families of polynomials that generalize the Kostka numbers. They are studied primarily in algebraic combinatorics and representation theory.
The two-variable Kostka polynomials Kλμ(q, t) are known by several names including Kostka–Foulkes polynomials, Macdonald–Kostka polynomials or q,t-Kostka polynomials. Here the indices λ and μ are integer partitions and Kλμ(q, t) is polynomial in the variables q and t. Sometimes one considers single-variable versions of these polynomials that arise by setting q = 0, i.e., by considering the polynomial Kλμ(t) = Kλμ(0, t).
There are two slightly different versions of them, one called transformed Kostka polynomials.[citation needed]
The one variable specializations of the Kostka polynomials can be used to express Hall-Littlewood polynomials Pμ as a linear combination of Schur polynomials sλ:
The Macdonald–Kostka polynomials can be used to express Macdonald polynomials (also denoted by Pμ) as a linear combination of Schur polynomials sλ:
where
Kostka numbers are special values of the 1 or 2 variable Kostka polynomials:
Examples
References
- Macdonald, I. G. (1995), Symmetric functions and Hall polynomials, Oxford Mathematical Monographs (2nd ed.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853489-1, MR 1354144
- Nelsen, Kendra; Ram, Arun (2003), "Kostka-Foulkes polynomials and Macdonald spherical functions", Surveys in combinatorics, 2003 (Bangor), London Math. Soc. Lecture Note Ser. 307, Cambridge: Cambridge Univ. Press, pp. 325–370, arXiv:math/0401298, MR 2011741
- Stembridge, J. R. (2005), Kostka-Foulkes Polynomials of General Type, lecture notes from AIM workshop on Generalized Kostka polynomials