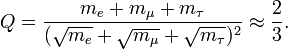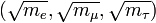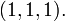Koide formula

From Wikipedia, the free encyclopedia

The Koide formula is an unexplained empirical equation discovered by Yoshio Koide in 1981. It relates the masses of the three charged leptons so well that it predicted the mass of the tau.

Formula

The Koide formula is:

Q={\frac {m_{e}+m_{{\mu }}+m_{{\tau }}}{({\sqrt {m_{e}}}+{\sqrt {m_{{\mu }}}}+{\sqrt {m_{{\tau }}}})^{2}}}\approx {\frac {2}{3}}.

It is clear that 1⁄3 < Q < 1. The superior bound follows if we assume that the square roots can not be negative. By Cauchy-Schwarz 1⁄3Q can be interpreted as the squared cosine of the angle between the vector

({\sqrt {m_{e}}},{\sqrt {m_{{\mu }}}},{\sqrt {m_{{\tau }}}})

and the vector

(1,1,1).

The mystery is in the physical value. The masses of the electron, muon, and tau are measured respectively as me = 0.510998910(13) MeV/c2, mμ = 105.658367(4) MeV/c2, and mτ = 1776.84(17) MeV/c2, where the digits in parentheses are the uncertainties in the last figures.[1] This gives Q = 0.666659(10).[2] Not only is this result odd in that three apparently random numbers should give a simple fraction, but also that Q is exactly halfway between the two extremes of 1⁄3 (should the three masses be equal) and 1 (should one mass dominate).

While the original formula appeared in the context of preon models, other ways have been found to produce it. As a whole, however, understanding remains incomplete.

Similar matches have been found for quarks depending on running masses, and for triplets of quarks not of the same flavour.[3][4][5] With alternating quarks, chaining Koide equations for consecutive triplets, it is possible to reach a result of 173.263947(6) GeV for the mass of the top quark.[6]

Running of particle masses

In quantum field theory, quantities like coupling constant and mass "run" with the energy scale. That is, their value depends on the energy scale at which the observation occurs, in a way described by a renormalization group equation (RGE). One usually expects relationships between such quantities to be simple at high energies (where some symmetry is unbroken) but not at low energies, where the RG flow will have produced complicated deviations from the high energy relation. The Koide relation is exact (within experimental error) for the pole masses, which are low-energy quantities defined at different energy scales. For this reason, many physicists regard the relation as "numerology" (e.g.[7]). However, the Japanese physicist Yukinari Sumino has constructed an effective field theory in which a new gauge symmetry causes the pole masses to exactly satisfy the relation.[8] Goffinet's doctoral thesis gives a discussion on pole masses and how the Koide formula can be reformulated without taking the square roots of masses.[9]

See also

Notes

  1. ↑ C. Amsler et. al. (Particle Data Group) (2008, and 2009 partial update). "Review of Particle Physics – Leptons". Physics Letters B 667 (1-5): 1. Bibcode:2008PhLB..667....1P. doi:10.1016/j.physletb.2008.07.018. 
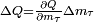  2. ↑ Since the uncertainties in me and mμ are much smaller than that in mτ, the uncertainty in Q was calculated as \scriptstyle {\Delta Q={\frac {\partial Q}{\partial m_{\tau }}}\Delta m_{\tau }}.
  3. ↑ Rodejohann, Werner; Zhang, He (2011). "Extension of an empirical charged lepton mass relation to the neutrino sector". Physics Letters B 698 (2): 152–156. arXiv:1101.5525. Bibcode:2011PhLB..698..152R. doi:10.1016/j.physletb.2011.03.007. 
  4. ↑ Rosen, Gerald (2007). "Heuristic development of a Dirac-Goldhaber model for lepton and quark structure" (PDF). Modern Phys. Lett. B 22 (4): 283–288. 
  5. ↑ Kartavtsev, Alexander (2011). A remark on the Koide relation for quarks. arXiv:1111.0480. Bibcode:2011arXiv1111.0480K. 
  6. ↑ Rivero, Alejandro. A new Koide tuple: strange-charm-bottom. arXiv:1111.7232. Bibcode:2011arXiv1111.7232R. 
  7. ↑ "Could the Koide formula be real?" by Luboš Motl, The Reference Frame blog, January 16, 2012.
  8. ↑ Y. Sumino (2009). "Family Gauge Symmetry as an Origin of Koide's Mass Formula and Charged Lepton Spectrum". JHEP 0905 (05): 075. arXiv:0812.2103. Bibcode:2009JHEP...05..075S. doi:10.1088/1126-6708/2009/05/075. 
  9. ↑ Goffinet, François (2008). "A bottom-up approach to fermion masses" (PDF). Université catholique de Louvain. 

References

Further reading

External links

  • Wolfram Alpha, link solves for the predicted tau mass from the Koide formula
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.