Kobayashi metric

In mathematics, the original Kobayashi metric is a pseudometric (or pseudodistance) on complex manifolds introduced by Kobayashi (1967). It can be viewed as the dual of the Carathéodory metric, and has been extended to complex analytic spaces and almost complex manifolds. On Teichmüller space the Kobayashi metric coincides with the Teichmüller metric; on the unit ball, it coincides with the Bergman metric.

An analogous pseudodistance was constructed for flat affine and projective structures in Kobayashi (1977) and then generalized to (normal) projective connections. Essentially the same construction has been applied to (normal, pseudo-Riemannian) conformal connections and, more recently, to general (regular) parabolic geometries.

Definition

If X is a complex manifold, the Kobayashi pseudometric d may be characterized as the largest pseudometric on X such that

,

for all holomorphic maps f from the unit disk D to X (where 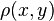denotes distance in the Poincaré metric on D).

References

• Kobayashi, Shoshichi (1967). "Intrinsic Metrics on Complex Manifolds". Bull. Amer. Math. Soc. 73: 347–349. 

• Kobayashi, Shoshichi (1970), Hyperbolic manifolds and holomorphic mappings, Pure and Applied Mathematics 2, New York: Marcel Dekker Inc., ISBN 978-0-8247-1380-5, MR 0277770 

• Kobayashi, Shoshichi (1977). "Intrinsic distances associated with flat affine or projective structures". J. Fac. Sci. Univ. Tokyo 24: 129–135. MR 445016. 

Further reading

• Lang, Serge (1986). "Hyperbolic and Diophantine anaysis". Bulletin of the American Mathematical Society 14 (2): 159–205. Zbl 0602.14019.