Knot tabulation

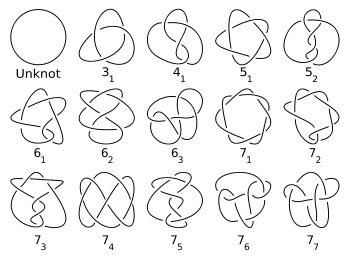
From Wikipedia, the free encyclopedia
A small table of all prime knots (excluding mirror images) with 7 crossings or less.

Ever since Sir William Thomson's vortex theory, mathematicians have tried to classify and tabulate all possible knots. As of May 2008, all prime knots up to 16 crossings have been tabulated.[1]

Beginnings

Main article: History of knot theory

In an attempt to make a periodic table of the elements, P. G. Tait, C. N. Little and others started counting all possible knots.[2]

Perko pair

Main article: Perko pair

In 1974 Perko discovered a duplication in the Tait-Little tables, called the Perko pair.

New methods

Jim Hoste, Jeff Weeks, and Morwen Thistlethwaite used computer searches to count all knots with 16 or fewer crossings. This research was performed separately using two different algorithms on different computers, lending support to the correctness of its results. Both counts found 1701936 prime knots (including the unknot) with up to 16 crossings.[1]

Starting with three crossings (the minimum for any nontrivial knot), the number of prime knots for each number of crossings is

1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988, 46972, 253293, 1388705, ... (sequence A002863 in OEIS)

See also

References

  1. ↑ 1.0 1.1 Hoste, Jim; Thistlethwaite, Morwen; Weeks, Jeff (1998), "The first 1,701,936 knots", The Mathematical Intelligencer 20 (4): 33–48, doi:10.1007/BF03025227, MR 1646740 .
  2. ↑ http://pzacad.pitzer.edu/~jhoste/HosteWebPages/downloads/Enumeration.pdf
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.