Knight's graph

From Wikipedia, the free encyclopedia
Knight's graph

8x8 Knight's graph
Vertices nm
Edges 4mn-6(m+n)+8
Girth 4 (if n≥3, m≥ 5)

In graph theory, a knight's graph, or a knight's tour graph, is a graph that represents all legal moves of the knight chess piece on a chessboard where each vertex represents a square on a chessboard and each edge is a legal move. More specifically, an n\times m knight's tour graph is a knight's tour graph of an n\times m chessboard.[1]

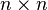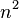For a n\times m knight's tour graph the total number of vertices is simply nm. For a n\times n knight's tour graph the total number of vertices is simply n^{2} and the total number of edges is 4(n-2)(n-1).[2]

A Hamiltonian path on the knight's tour graph is a knight's tour.[1] Schwenk's theorem characterizes the sizes of chessboard for which a knight's tour exist.[3]

References

  1. ↑ 1.0 1.1 Averbach, Bonnie; Chein, Orin (1980), Problem Solving Through Recreational Mathematics, Dover, p. 195, ISBN 9780486131740 .
  2. ↑ "Sloane's A033996 ", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  3. ↑ Watkins, John J. (2012), Across the Board: The Mathematics of Chessboard Problems. Paradoxes, perplexities, and mathematical conundrums for the serious head scratcher, Princeton University Press, p. 44, ISBN 9780691154985 .

See also

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.