Kirkendall effect
The Kirkendall effect is the motion Boundary of layer between two metals that occurs as a consequence of the difference in diffusion rates of the metal atoms. The effect can be observed for example by placing insoluble markers at the interface between a pure metal and an alloy containing that metal, and heating to a temperature where atomic diffusion is possible; the boundary will move relative to the markers.
This process was named after Ernest Kirkendall (1914–2005) assistant professor of chemical engineering at Wayne State University from 1941 to 1946. He discovered the effect in 1947.[1]
The Kirkendall effect has important practical consequences. One of these is the prevention or suppression of voids formed at the boundary interface in various kinds of alloy to metal bonding. These are referred to as Kirkendall voids.
In 1972, C.W. Horsting of the RCA Corporation published a paper which reported test results on the reliability of semiconductor devices in which the connections were made using aluminium wires bonded ultrasonically to gold plated posts. His paper demonstrated the importance of the Kirkendall effect in wire bonding technology, but also showed the significant contribution of any impurities present to the rate at which precipitation occurred at the wire bonds. Two of the important contaminants that have this effect, known as Horsting effect (Horsting voids) are fluorine and chlorine. Both Kirkendall voids and Horsting voids are known causes of wire bond fractures, though historically this cause is often confused with the purple colored appearance of one of the five different gold-aluminium intermetallics, commonly referred to as "purple plague" and less often "white plague".[2]
History
The Kirkendall effect was discovered by Ernest Kirkendall and Alice Smigelskas in 1947, in the course of Kirkendall’s ongoing research into diffusion in brass.[3] The paper in which he discovered the famous effect was the third in his series of papers on brass diffusion, the first being his thesis. His second paper revealed that zinc diffused more quickly than copper in alpha-brass, which led to the research producing his revolutionary theory. Until this point, substitutional and ring methods were the dominant ideas for diffusional motion. Kirkendall’s experiment produced evidence of a vacancy diffusion mechanism, which is the accepted mechanism to this day. At the time it was submitted, the paper and Kirkendall’s ideas were rejected from publication by Robert Franklin Mehl, director of the Metals Research Laboratory at Carnegie Institute of Technology. Mehl refused to accept Kirkendall’s evidence of this new diffusion mechanism, and denied publication for over six months, only relenting after a conference was held and several other researchers confirmed Kirkendall’s results.[3]
Kirkendall's experiment
A bar of brass (70% Cu, 30% Zn) was used as a core, with molybdenum wires stretched along its length, and then coated in a layer of pure copper. Molybdenum was chosen as the marker material due to it being very insoluble in brass, eliminating any error due to the markers diffusing themselves. Diffusion was allowed to take place at 785°C over the course of 56 days, with cross-sections being taken at six times throughout the span of the experiment. Over time, it was observed that the wire markers moved closer together as the zinc diffused out of the brass and into the copper. A difference in location of the interface was visible in cross sections of different times. Compositional change of the material from diffusion was confirmed by x-ray diffraction.[1]
Diffusion mechanism
Early diffusion models postulated that atomic motion in substitutional alloys occurs via a direct exchange mechanism, in which atoms migrate by switching positions with atoms on adjacent lattice sites.[4] Such a mechanism implies that the atomic fluxes of two different materials across an interface must be equal, as each atom moving across the interface causes another atom to move across in the other direction.
Another possible diffusion mechanism involves lattice vacancies. An atom can move into a vacant lattice site, effectively causing the atom and the vacancy to switch places. If large-scale diffusion takes place in a material, there will be a flux of atoms in one direction and a flux of vacancies in the other.
The Kirkendall effect arises when two distinct materials are placed next to each other and diffusion is allowed to take place between them. In general, the diffusion coefficients of the two materials in each other are not the same. This is only possible if diffusion occurs by a vacancy mechanism; with an exchange mechanism, atoms will cross the interface in pairs, so the diffusion rates will be identical. The material with the higher diffusion coefficient will have a larger associated vacancy flux into it, so the net movement of vacancies will be from the material with the lower diffusion coefficient into the material with the higher diffusion coefficient.[4]
Macroscopic evidence for the Kirkendall effect can be gathered by placing inert markers at the initial interface between the two materials, such as molybdenum markers at an interface between copper and brass. The diffusion coefficient of zinc is higher than the diffusion coefficient of copper in this case. Since zinc atoms leave the brass at a higher rate than copper atoms enter, the size of the brass region decreases as diffusion progresses. Relative to the molybdenum markers, the copper-brass interface moves toward the brass at an experimentally measurable rate.[1]
Darken's equations
Shortly after the publication of Kirkendall’s paper, L.S. Darken published an analysis of diffusion in binary systems much like the one studied by Smigelskas and Kirkendall. By separating the actual diffusive flux of the materials from the movement of the interface relative to the markers, Darken found the marker velocity  to be[5]
to be[5]
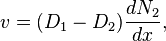
where  and
and  are the diffusion coefficients of the two materials and
are the diffusion coefficients of the two materials and  is an atomic fraction.
One consequence of this equation is that the movement of an interface varies linearly with the square root of time, which is exactly the experimental relationship discovered by Smigelskas and Kirkendall.[1]
is an atomic fraction.
One consequence of this equation is that the movement of an interface varies linearly with the square root of time, which is exactly the experimental relationship discovered by Smigelskas and Kirkendall.[1]
Darken also developed a second equation that defines a combined chemical diffusion coefficient  in terms of the diffusion coefficients of the two interfacing materials:[5]
in terms of the diffusion coefficients of the two interfacing materials:[5]
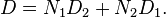
This chemical diffusion coefficient can be used to mathematically analyze Kirkendall effect diffusion via the Boltzmann-Matano method.
Kirkendall porosity
One important consideration deriving from Kirkendall’s work is the presence of pores formed during diffusion. These voids act as sinks for vacancies, and when enough accumulate they can become substantial and expand in an attempt to restore equilibrium. Porosity occurs due to the difference in diffusion rate of the two species.[6]
Pores in metals have ramifications for mechanical, thermal, and electrical properties, and thus control over their formation is often desired. The equation[7]

where  is the distance moved by a marker,
is the distance moved by a marker,  is a coefficient determined by intrinsic diffusivities of the materials, and
is a coefficient determined by intrinsic diffusivities of the materials, and 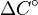 is a concentration difference between components, has proven to be an effective model for mitigating Kirkendall porosity. Controlling annealing temperature is another method of reducing or eliminating porosity. Kirkendall porosity typically occurs at a set temperature in a system, so annealing can be performed at lower temperatures for longer times to avoid formation of pores.[8]
is a concentration difference between components, has proven to be an effective model for mitigating Kirkendall porosity. Controlling annealing temperature is another method of reducing or eliminating porosity. Kirkendall porosity typically occurs at a set temperature in a system, so annealing can be performed at lower temperatures for longer times to avoid formation of pores.[8]
Nanotechnology applications
The Catalan Institute of Nanotechnology in Bellaterra, Spain has developed a chemical process creating hollows in nano-particles and forming double-walled boxes and multi-chambered tubes. The results of the study have appeared in the journal Science.[9]
Minute silver cubes were treated with cationic gold which at room temperatures led to a loss of electrons from the silver atoms which were taken up by an electrolytic solution. The gaining of electrons transformed the cationic gold into metallic gold which then attached to the surface of the silver cube. This covering protects the underlying silver, confining the reaction to the uncoated parts. Finally, there remains only a single hole on the surface through which the reaction enters the cube. A secondary effect then takes place when silver atoms from inside the cube begin to migrate through the hole to the gold on the surface, creating a void inside the cube.
The process will have a wide range of applications. Small changes in the chemical environment will allow control of reaction and diffusion at room temperatures, permitting manufacture of diverse polymetallic hollow nanoparticles through galvanic replacement and the Kirkendall effect.[10]
See also
References
- ↑ 1.0 1.1 1.2 1.3 Smigelskas, A. D.; Kirkendall, E. O. (1947). "Zinc Diffusion in Alpha Brass". Trans. AIME 171: 130–142.
- ↑ "Contamination-Enhanced Growth of Au/Al Intermetallic and Horsting Voids". NASA. Retrieved 28 April 2013.
- ↑ 3.0 3.1 Nakajima, Hideo (1997). "The Discovery and Acceptance of the Kirkendall Effect: The Result of a Short Research Career". JOM 49 (6): 15–19. Retrieved 28 April 2013.
- ↑ 4.0 4.1 Bhadeshia, H.K.D.H. "The Kirkendall Effect". University of Cambridge. Retrieved 28 April 2013.
- ↑ 5.0 5.1 Darken, L.S. (February 1948). "Diffusion, Mobility, and Their Interrelation through Free Energy in Binary Metallic Systems". Trans. AIME 175: 194.
- ↑ Seitz, F. (May 1953). "On the porosity observed in the Kirkendall effect". Acta Metallurgica 1 (3): 355–369. doi:10.1016/0001-6160(53)90112-6. Retrieved 28 April 2013.
- ↑ Son, Yoon-Ho; J.E. Morral (November 1989). "The Effect of Composition on Marker Movement and Kirkendall Porosity in Ternary Alloys". Metallurgical Transactions A 20A: 2299–2303. Retrieved 28 April 2013.
- ↑ Cogan, S.F.; S. Kwon, J.D. Klein, R.M. Rose (May 1983). "Fabrication of Large Diameter External-Diffusion Processed Nb3Sn Composites". IEEE Transactions on Magnetics. Mag-19 (3): 1139–1142.
- ↑ "Nanoparticle hollowing method promises medical advances". BBC News. 8 December 2011.
- ↑ http://www.sciencemag.org/content/334/6061/1377.abstract?sid=1055ee45-abc7-4f9a-8698-e9ae3487aa68
External links
- Kirkendall Effect: Dramatic History of Discovery and Developments by L.N. Paritskaya
- Interdiffusion and Kirkendall Effect in Cu-Sn Alloys
- Kirkendall Effect and Mechanism of Self-Diffusion in B2 Intermetallic Compounds
- Visual demonstration of the Kirkendall effect