King's graph

From Wikipedia, the free encyclopedia
King's graph

8x8 King's graph
Vertices nm
Edges 4nm-3(n+m)+2

In graph theory, a king's graph is a graph that represents all legal moves of the king chess piece on a chessboard where each vertex represents a square on a chessboard and each edge is a legal move. More specifically, an n\times m king's graph is a king's graph of an n\times m chessboard.[1]

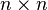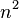For a n\times m king's graph the total number of vertices is simply nm. For a n\times n king's graph the total number of vertices is simply n^{2} and the total number of edges is (2n-2)(2n-1).[2]

The neighbourhood of a vertex in the king's graph corresponds to the Moore neighborhood for cellular automata.[3] A generalization of the king's graph, called a kinggraph, is formed from a squaregraph (a planar graph in which each bounded face is a quadrilateral and each interior vertex has at least four neighbors) by adding the two diagonals of every quadrilateral face of the squaregraph.[4]

References

  1. ↑ Chang, Gerard J. (1998), "Algorithmic aspects of domination in graphs", in Du, Ding-Zhu; Pardalos, Panos M., Handbook of combinatorial optimization, Vol. 3, Boston, MA: Kluwer Acad. Publ., pp. 339–405, MR 1665419 . Chang defines the king's graph on p. 341.
  2. ↑ "Sloane's A002943 ", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  3. ↑ Smith, Alvy Ray (1971), "Two-dimensional formal languages and pattern recognition by cellular automata", 12th Annual Symposium on Switching and Automata Theory, pp. 144–152, doi:10.1109/SWAT.1971.29 .
  4. ↑ Chepoi, Victor; Dragan, Feodor; Vaxès, Yann (2002), "Center and diameter problems in plane triangulations and quadrangulations", Proceedings of the Thirteenth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '02), pp. 346–355 .

See also

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.