Kinetic heap

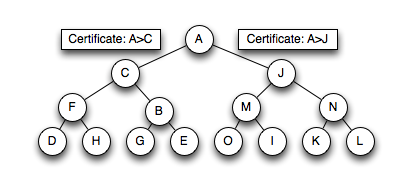
From Wikipedia, the free encyclopedia

A Kinetic Heap is a kinetic data structure, obtained by the kinetization of a heap. It is designed to store elements (keys associated with priorities) where the priority is changing as a continuous function of time. As a type of kinetic priority queue, it maintains the maximum priority element stored in it. The kinetic heap data structure works by storing the elements as a tree that satisfies the following heap property - if <var>B</var> is a child node of <var>A</var>, then the priority of the element in <var>A</var> must be higher than the priority of the element in <var>B</var>. This heap property is enforced using certificates along every edge so, like other kinetic data structures, a kinetic heap also contains a priority queue (the event queue) to maintain certificate failure times.

Implementation and operations

A regular heap can be kinetized by augmenting with a certificate [<var>A</var>><var>B</var>] for every pair of nodes<var>A</var>, <var>B</var> such that <var>B</var> is a child node of <var>A</var>. If the value stored at a node <var>X</var> is a function f<var>X</var>(<var>t</var>) of time, then this certificate is only valid while f<var>A</var>(<var>t</var>) > f<var>B</var>(<var>t</var>). Thus, the failure of this certificate must be scheduled in the event queue at a time <var>t</var> such that f<var>A</var>(<var>t</var>) > f<var>B</var>(<var>t</var>).

All certificate failures are scheduled on the "event queue", which is assumed to be an efficient priority queue whose operations take O(log <var>n</var>) time.

Dealing with certificate failures

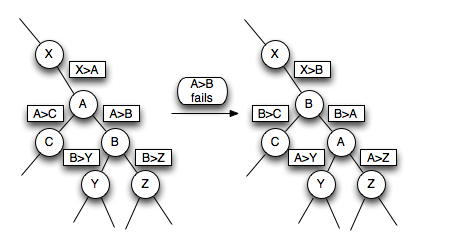
When a certificate [<var>A</var>><var>B</var>] fails, the data structure must swap <var>A</var> and <var>B</var> in the heap, and update the certificates that each of them was present in.

For example, if B (call its child nodes Y,Z) was a child node of A (call its child nodesB,C and its parent node X), and the certificate [<var>A</var>><var>B</var>] fails, then the data structure must swapB and A, then replace the old certificates (and the corresponding scheduled events) [<var>A</var>><var>B</var>], [<var>A</var><<var>X</var>], [<var>A</var>><var>C</var>], [<var>B</var>><var>Y</var>], [<var>B</var>><var>Z</var>] with new certificates [<var>B</var>><var>A</var>], [<var>B</var><<var>X</var>], [<var>B</var>><var>C</var>], [<var>A</var>><var>Y</var>] and [<var>A</var>><var>Z</var>].

Thus, assuming non-degeneracy of the events (no two events happen at the same time), only a constant number of events need to be de-scheduled and re-scheduled even in the worst case.

Operations

A kinetic heap supports the following operations:

  • create-heap(<var>h</var>): create an empty kinetic heap <var>h</var>
  • find-max(<var>h, t</var>) (or find-min): - return the max (or min for a min-heap) value stored in the heap <var>h</var> at the current virtual time <var>t</var>.
  • insert(<var>X</var>, f<var>X</var>, <var>t<var>): - insert a key <var>X</var> into the kinetic heap at the current virtual time <var>t</var>, whose value changes as a continuous function f<var>X</var>(<var>t</var>) of time <var>t</var>. The insertion is done as in a normal heap in O(log <var>n</var>) time, but O(log <var>n</var>) certificates might need to be changed as a result, so the total time for rescheduling certificate failures is O(log 2 <var>n</var>)
  • delete(<var>X</var>, <var>t</var>) - delete a key at the current virtual time <var>t</var>. The deletion is done as in a normal heap in O(log <var>n</var>) time, but O(log <var>n</var>) certificates might need to be changed as a result, so the total time for rescheduling certificate failures is O(log 2 <var>n</var>).

Performance

Kinetic heaps perform well according to the four metrics (responsiveness, locality, compactness and efficiency) of kinetic data structure quality defined by Basch et al.[1] The analysis of the first three qualities is straightforward:

  • Responsiveness:A kinetic heap is responsive, since each certificate failure causes the concerned keys to be swapped and leads to only five certificates being replaced in the worst case.
  • Locality: Each node is present in one certificate each along with its parent node and two child nodes (if present), meaning that each node can be involved in a total of three scheduled events in the worst case, thus kinetic heaps are local.
  • Compactness: Each edge in the heap corresponds to exactly one scheduled event, therefore the number of scheduled events is exactly where <var>n</var> is the number of nodes in the kinetic heap. Thus, kinetic heaps are compact.

Analysis of efficiency

The efficiency of a kinetic heap in the general case is largely unknown.[1][2][3]However, in the special case of affine motion f(<var>t</var>) = a<var>t</var> + b of the priorities, kinetic heaps are known to be very efficient.[2]

Affine motion, no insertions or deletions

In this special case, the maximum number of events processed by a kinetic heap can be shown to be exactly the number of edges in the transitive closure of the tree structure of the heap, which is O(<var>n</var>log<var>n</var>) for a tree of height O(log<var>n</var>) [2]

Affine motion, with insertions and deletions

If <var>n</var> insertions and deletions are made on a kinetic heap that starts empty, the maximum number of events processed is 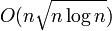O(n{\sqrt {n\log n}}).[4] However, this bound is not believed to be tight,[2] and the only known lower bound is 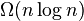\Omega (n\log n).[4]

Variants

This article deals with "simple" kinetic heaps as described above, but other variants have been developed for specialized applications,[5] such as:

  • Fibonacci kinetic heap
  • Incremental kinetic heap

Other heap-like kinetic priority queues are:

References

  1. ↑ 1.0 1.1 Basch, J., Guibas, L. J., Hershberger, J (1997). "Data structures for mobile data". Proceedings of the eighth annual ACM-SIAM symposium on Discrete algorithms. SODA. Society for Industrial and Applied Mathematics. pp. 747 –756. Retrieved May 17, 2012. 
  2. ↑ 2.0 2.1 2.2 2.3 da Fonseca, Guilherme D. and de Figueiredo, Celina M. H. "Kinetic heap-ordered trees: Tight analysis and improved algorithms". Information Processing Letters. pp. 165–169. Retrieved May 17, 2012. 
  3. ↑ da Fonseca, Guilherme D. and de Figueiredo, Celina M. H. and Carvalho, Paulo C. P. "Kinetic hanger". Information Processing Letters. pp. 151–157. Retrieved May 17, 2012. 
  4. ↑ 4.0 4.1 Basch, J, Guibas, L. J., Ramkumar, G. D. (1997). "Sweeping lines and line segments with a heap". Proceedings of the thirteenth annual symposium on Computational geometry. SCG. ACM. pp. 469–471. Retrieved May 17, 2012. 
  5. ↑ K. H., Tarjan, R. and T. K. (2001). "Faster kinetic heaps and their use in broadcast scheduling". Proc. 12th ACM-SIAM Symposium on Discrete Algorithms. ACM. pp. 836–844. 

Guibas, Leonidas. "Kinetic Data Structures - Handbook". Retrieved May 17, 2012. 

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.