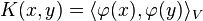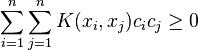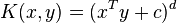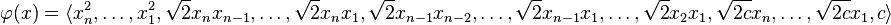Kernel trick

From Wikipedia, the free encyclopedia

For machine learning algorithms, the kernel trick is a way of mapping observations from a general set S into an inner product space V (equipped with its natural norm), without having to compute the mapping explicitly, because the observations will gain meaningful linear structure in V. Linear classifications in V are equivalent to generic classifications in S. The trick or method used to avoid the explicit mapping is to use learning algorithms that only require dot products between the vectors in V, and choose the mapping such that these high-dimensional dot products can be computed within the original space, by means of a kernel function.

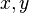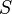For $x,y$ on $S$ , certain functions 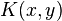$K(x,y)$ can be expressed as an inner product (usually in a different space). K is often referred to as a kernel or a kernel function. The word kernel is used in different ways throughout mathematics.

If one is insightful regarding a particular machine learning problem, one may manually construct 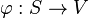$\varphi :S\to V$ such that

$K(x,y)=\langle \varphi (x),\varphi (y)\rangle _{V}$

and verify that 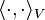$\langle \cdot ,\cdot \rangle _{V}$ is indeed an inner product.

Furthermore, an explicit representation for $\varphi$ is not required: it suffices to know that V is an inner product space. Conveniently, based on Mercer's theorem, it suffices to equip S with one's choice of measure and verify that in fact, $K:S\times S\to {\mathbb {R}}$ satisfies Mercer's condition.

Mercer's theorem is stated in a general mathematical setting with implications in the theory of integral equations. However, the general statement is more than what is required for understanding the kernel trick. Given a finite observation set S, one can select the counting measure 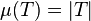$\mu (T)=|T|$ for all 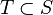$T\subset S$ . Then the integral in Mercer's theorem reduces to a simple summation

$\sum _{{i=1}}^{n}\sum _{{j=1}}^{n}K(x_{i},x_{j})c_{i}c_{j}\geq 0$

for all finite sequences of points x₁, ..., x_n of S and all choices of real numbers c₁, ..., c_n (cf. positive definite kernel).

Some algorithms that depend on arbitrary relationships in the native space would, in fact, have a linear interpretation in a different setting: the range space of $\varphi$ . The linear interpretation gives us insight about the algorithm. Furthermore, there is often no need to compute $\varphi$ directly during computation, as is the case with support vector machines. Some cite this running time shortcut as the primary benefit. Researchers also use it to justify the meanings and properties of existing algorithms.

The kernel trick was first published in 1964 by Aizerman et al.^[1]

Theoretically, a kernel matrix K must be positive semi-definite (PSD).^[2] Empirically, for machine learning heuristics, choices of K that do not satisfy Mercer's condition may still perform reasonably if K at least approximates the intuitive idea of similarity.^[3] Regardless of whether K is a Mercer kernel, K can still be referred to a "kernel". Suppose K is any square matrix, then 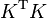$K^{{\mathrm {T}}}K$ is a PSD matrix.

Applications

It has been applied to several kinds of algorithm in machine learning and statistics, including:

Commonly used kernels in such algorithms include the RBF and polynomial kernels, representing a mapping of vectors in ${\mathcal {R}}^{n}$ into a much richer feature space over degree- $d$ polynomials of the original variables:^[4]

$K(x,y)=(x^{T}y+c)^{d}$

where $c\geq 0$ is a constant trading off the influence of higher-order versus lower-order terms in the polynomial. For $d=2$ , this $K$ is the inner product in a feature space induced by the mapping

$\varphi (x)=\langle x_{n}^{2},\ldots ,x_{1}^{2},{\sqrt {2}}x_{n}x_{{n-1}},\ldots ,{\sqrt {2}}x_{n}x_{1},{\sqrt {2}}x_{{n-1}}x_{{n-2}},\ldots ,{\sqrt {2}}x_{{n-1}}x_{{1}},\ldots ,{\sqrt {2}}x_{{2}}x_{{1}},{\sqrt {2c}}x_{n},\ldots ,{\sqrt {2c}}x_{1},c\rangle$

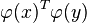The kernel trick here lies in working in an $\left({\binom {n+2}{2}}={\frac {n^{2}+3n+2}{2}}\right)$ -dimensional space, without ever explicitly transforming the original data points into that space, but instead relying on algorithms that only need to compute inner products $\varphi (x)^{T}\varphi (y)$ within that space, which are identical to 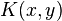$K(x,y)$ and can thus cheaply be computed in the original space using only $n+1$ multiplications.

References

↑ M. Aizerman, E. Braverman, and L. Rozonoer (1964). "Theoretical foundations of the potential function method in pattern recognition learning". Automation and Remote Control 25: 821–837.
↑ Mehryar Mohri, Afshin Rostamizadeh, Ameet Talwalkar (2012) Foundations of Machine Learning, The MIT Press ISBN 9780262018258.
↑ http://www.svms.org/mercer/
↑ http://www.cs.tufts.edu/~roni/Teaching/CLT2008S/LN/lecture18.pdf

Kernel trick

Applications

References

External links

See also