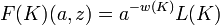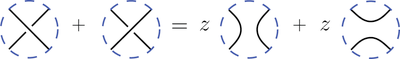Kauffman polynomial
In knot theory, the Kauffman polynomial is a 2-variable knot polynomial due to Louis Kauffman. It is initially defined on a link diagram as
where 
is the writhe of the link diagram and 
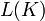is a polynomial in a and z defined on link diagrams by the following properties:
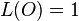(O is the unknot)
- L is unchanged under type II and III Reidemeister moves
Here 
is a strand and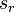 
(resp. 
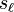) is the same strand with a right-handed (resp. left-handed) curl added (using a type I Reidemeister move).
Additionally L must satisfy Kauffman's skein relation:
The pictures represent the L polynomial of the diagrams which differ inside a disc as shown but are identical outside.
Kauffman showed that L exists and is a regular isotopy invariant of unoriented links. It follows easily that F is an ambient isotopy invariant of oriented links.
The Jones polynomial is a special case of the Kauffman polynomial, as the L polynomial specializes to the bracket polynomial. The Kauffman polynomial is related to Chern-Simons gauge theories for SO(N) in the same way that the HOMFLY polynomial is related to Chern-Simons gauge theories for SU(N) (see Witten's article "Quantum field theory and the Jones polynomial", in Commun. Math. Phys.)
Further reading
- Louis Kauffman, On Knots, (1987), ISBN 0-691-08435-1
External links
- Springer EoM entry for Kauffman polynomial
- "The_Kauffman_Polynomial", The Knot Atlas.
| |||||||||||||||||||||||
