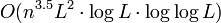Karmarkar's algorithm

From Wikipedia, the free encyclopedia

Karmarkar's algorithm is an algorithm introduced by Narendra Karmarkar in 1984 for solving linear programming problems. It was the first reasonably efficient algorithm that solves these problems in polynomial time. The ellipsoid method is also polynomial time but proved to be inefficient in practice.

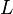Where n is the number of variables and L is the number of bits of input to the algorithm, Karmarkar's algorithm requires O(n^{{3.5}}L) operations on O(L) digit numbers, as compared to O(n^{6}L) such operations for the ellipsoid algorithm. The runtime of Karmarkar's algorithm is thus

O(n^{{3.5}}L^{2}\cdot \log L\cdot \log \log L)

using FFT-based multiplication (see Big O notation).

Karmarkar's algorithm falls within the class of interior point methods: the current guess for the solution does not follow the boundary of the feasible set as in the simplex method, but it moves through the interior of the feasible region, improving the approximation of the optimal solution by a definite fraction with every iteration, and converging to an optimal solution with rational data.[1]

The Algorithm

Consider a Linear Programming problem in matrix form:

maximize cTx
subject to Ax ≤ b.

The algorithm determines the next feasible direction toward optimality and scales back by a factor 0 < γ ≤ 1.

Karmarkar's algorithm is rather complicated. A simplified version, called the affine-scaling method, proposed and analyzed by others,[2] can be described succinctly as follows. Note that the affine-scaling algorithm, while efficient in practice, is not a polynomial time algorithm.

Algorithm Affine-Scaling
  Input:  A, b, c, x^{0}, stopping criterion, \gamma .
  k\leftarrow 0
  do while stopping criterion not satisfied
     v^{k}\leftarrow b-Ax^{k}
     D_{v}\leftarrow \operatorname {diag}(v_{1}^{k},\ldots ,v_{m}^{k})
     h_{x}\leftarrow (A^{T}D_{v}^{{-2}}A)^{{-1}}c
     h_{v}\leftarrow -Ah_{x}
     if h_{v}\geq 0 then
        return unbounded
     end if
     \alpha \leftarrow \gamma \cdot \min\{-v_{i}^{k}/(h_{v})_{i}\,\,|\,\,(h_{v})_{i}<0,\,i=1,\ldots ,m\}
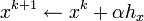
     x^{{k+1}}\leftarrow x^{k}+\alpha h_{x}
     k\leftarrow k+1
  end do
  • "←" is a shorthand for "changes to". For instance, "largest ← item" means that the value of largest changes to the value of item.
  • "return" terminates the algorithm and outputs the value that follows.

Example

Example solution

Consider the linear program

maximize x_{1} + x_{2}
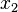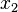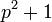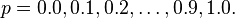subject to 2px_{1} + x_{2} \leq p^{2}+1, p=0.0,0.1,0.2,\ldots ,0.9,1.0.

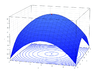
That is, there are 2 variables 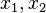x_{1},x_{2} and 11 constraints associated with varying values of p. This figure shows each iteration of the algorithm as red circle points. The constraints are shown as blue lines.

Patent controversy

At the time he invented the algorithm, Narendra Karmarkar was employed by AT&T and they realized that his invention could be of practical importance. In April 1985, AT&T promptly applied for a patent on Karmarkar's algorithm and that became more fuel for the ongoing controversy over the issue of software patents.[3] This left many mathematicians uneasy, such as Ronald Rivest (himself one of the holders of the patent on the RSA algorithm), who expressed the opinion that research proceeded on the basis that algorithms should be free. Even before the patent was actually granted, it seemed that there was prior art that might have been applicable.[4] Mathematicians who specialize in numerical analysis such as Philip Gill and others showed that Karmarkar's algorithm is actually equivalent to a projected Newton barrier method with a logarithmic barrier function, if the parameters are chosen suitably.[5] Methods referred to by Gill were widely used for nonlinear programming since the 1960s. In fact, one well-known book first published in 1968 described the technique specifically in the context of linear programming.[6] However, some say Gill's argument is flawed, insofar as the method they describe does not even qualify as an "algorithm", since it requires choices of parameters that don't follow from the internal logic of the method, but rely on external guidance, essentially from Karmarkar's algorithm.[7] Furthermore, Karmarkar's contributions are considered far from obvious in light of all prior work, including Fiacco-McCormick, Gill and others cited by Saltzman.[7][8][9] The patent was eventually granted as U.S. Patent 4,744,026: "Methods and apparatus for efficient resource allocation" in May 1988. The patent, however, proved to be of limited commercial value to AT&T. They built up the KORBX[10] system, an 8-processor Alliant computer incorporating linear programming software using Karmarkar's algorithm, priced at US$8.9 million each, and they only managed to sell two such systems.[4] Opponents of software patents have further alleged that the patents ruined the positive interaction cycles that previously characterized the relationship between researchers in linear programming and industry, and specifically it isolated Karmarkar himself from the network of mathematical researchers in his field. [11]

The patent itself expired in April 2006, and the algorithm is presently in the public domain.

References

  1. ↑ Strang, Gilbert (1 June 1987). "Karmarkar’s algorithm and its place in applied mathematics". The Mathematical Intelligencer (New York: Springer) 9 (2): 4–10. doi:10.1007/BF03025891. ISSN 0343-6993. MR '''883185'''. 
  2. ↑ Robert J. Vanderbei; Meketon, Marc, Freedman, Barry (1986). "A Modification of Karmarkar's Linear Programming Algorithm". Algorithmica 1: 395–407. doi:10.1007/BF01840454. 
  3. ↑ Kolata, Gina (1989-03-12). "IDEAS & TRENDS; Mathematicians Are Troubled by Claims on Their Recipes". The New York Times. 
  4. ↑ 4.0 4.1 Various posts by Matthew Saltzman, Clemson University
  5. ↑ Gill, Philip E.; Murray, Walter, Saunders, Michael A., Tomlin, J. A. and Wright, Margaret H. (1986). "On projected Newton barrier methods for linear programming and an equivalence to Karmarkar’s projective method". Mathematical Programming 36 (2): 183–209. doi:10.1007/BF02592025. 
  6. ↑ Anthony V. Fiacco; Garth P. McCormick (1968). Nonlinear Programming: Sequential Unconstrained Minimization Techniques. New York: Wiley. ISBN 978-0-471-25810-0.  Reprinted by SIAM in 1990 as ISBN 978-0-89871-254-4.
  7. ↑ 7.0 7.1 Andrew Chin (2009). "On Abstraction and Equivalence in Software Patent Doctrine: A Response to Bessen, Meurer and Klemens". Journal Of Intellectual Property Law 16: 214–223. 
  8. ↑ Mark A. Paley (1995). "The Karmarkar Patent: Why Congress Should “Open the Door” to Algorithms as Patentable Subject Matter". 22 COMPUTER L. REP. 7
  9. ↑ Margaret H. Wright (2004). "The Interior-Point Revolution in Optimization: History, Recent Developments, and Lasting Consequences". Bulletins of the American Mathematical Society 42: 39–56. 
  10. ↑ Marc S. Meketon; Y.C. Cheng, D.J. Houck, J.M.Liu, L. Slutsman, Robert J. Vanderbei, and P. Wang (1989). "The AT&T KORBX System". AT&T Technical Journal 68: 7–19. 
  11. ↑ "今野浩: カーマーカー特許とソフトウェア – 数学は 特許に なるか (Konno Hiroshi: The Kamarkar Patent and Software – Has Mathematics Become Patentable?)". FFII. Retrieved 2008-06-27. 
Optimization: Algorithms, methods, and heuristics
The graph of a strictly concave quadratic function is shown in blue, with its unique maximum shown as a red dot. Below the graph appears the contours of the function: The level sets are nested ellipses.
 
Convex
minimization
Linear and
quadratic
Interior point
Basis-Exchange
  • Categories
    • Algorithms and methods
    • Heuristics
  • Software
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.