Karel Lambert
Karel Lambert (born 1928) is a philosopher and logician at the University of California, Irvine and the University of Salzburg. He has written extensively on the subject of free logic, a term which he coined.[1]
Lambert's Law
Lambert's Law is the major principle in any free definite description theory that says: For all x, x = the y (A) if and only if (A(x/y) & for all y (if A then y = x)). Free logic itself is an adjustment of a given standard predicate logic such as to relieve it of existential assumptions, and so make it a free logic. Taking Bertrand Russell's predicate logic in his Principia Mathematica as standard, one replaces universal instantiation,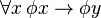 
, with universal specification 
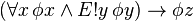. Thus universal statements, like "All men are mortal," or "Everything is a unicorn," do not presuppose that there are men or that there is anything. These would be symbolized, with the appropriate predicates, as 
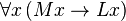and 
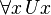, which in Principia Mathematica entail 
and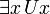 
, but not in free logic. The truth of these last statements, when used in a free logic, depend on the domain of quantification, which may be the null set.
Published works
- Philosophical Applications of Free Logic "A Theory of Definite Descriptions" (1991) details an account of Russell's Theory of Descriptions in free logic. In the process, he demonstrates how a formulation from Hintikka allows for a contradiction by a correlate in logic to Russell's Paradox. He introduces the predicate
External links
References
- ↑ Lambert, Karel (1960). "The Definition of E! in Free Logic". Abstracts: The International Congress for Logic, Methodology and Philosophy of Science (Palo Alto, CA: Stanford University Press).
|