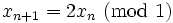Kaplan–Yorke map

From Wikipedia, the free encyclopedia

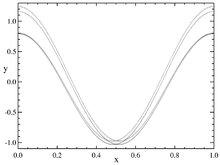
A plot of 100,000 iterations of the Kaplan-Yorke map with α=0.2. The initial value (x₀,y₀) was (128873/350377,0.667751).

The Kaplan–Yorke map is a discrete-time dynamical system. It is an example of a dynamical system that exhibits chaotic behavior. The Kaplan–Yorke map takes a point (x_n, y_n ) in the plane and maps it to a new point given by

$x_{{n+1}}=2x_{n}\ ({\textrm {mod}}~1)\,$

$y_{{n+1}}=\alpha y_{n}+\cos(4\pi x_{n})\,$

where mod is the modulo operator with real arguments. The map depends on only the one constant α.

Calculation method

Due to roundoff error, successive applications of the modulo operator will yield zero after some ten or twenty iterations when implemented as a floating point operation on a computer. It is better to implement the following equivalent algorithm:

$a_{{n+1}}=2a_{n}\ ({\textrm {mod}}~b)\,$

$x_{{n+1}}=a_{n}/b\,$

$y_{{n+1}}=\alpha y_{n}+\cos(4\pi x_{n})\,$

where the $a_{n}$ and $b$ are computational integers. It is also best to choose $b$ to be a large prime number in order to get many different values of $x_{n}$ .

References

J.L. Kaplan and J.A. Yorke (1979). H.O. Peitgen and H.O. Walther, ed. Functional Differential Equations and Approximations of Fixed Points (Lecture notes in Mathematics 730). Springer-Verlag. ISBN 0-387-09518-7.
P. Grassberger and I. Procaccia (1983). "Measuring the strangeness of strange attractors". Physica 9D (1-2): 189–208. Bibcode:1983PhyD....9..189G. doi:10.1016/0167-2789(83)90298-1.

v t e Chaos theory

Chaos theory	Anosov diffeomorphism Bifurcation theory Butterfly effect Chaos theory in organizational development Complexity Control of chaos Dynamical system Edge of chaos Fractal Predictability Quantum chaos Santa Fe Institute Synchronization of chaos Unintended consequences

Chaotic maps (list)	Arnold tongue Arnold's cat map Baker's map Chua's circuit Complex quadratic map Complex squaring map Coupled map lattice Double pendulum Duffing equation Duffing map Dyadic transformation Dynamical billiards outer Exponential map Gauss map Gingerbreadman map Hénon map Horseshoe map Ikeda map Interval exchange map Kaplan–Yorke map Logistic map Lorenz system Rabinovich–Fabrikant equations Rössler attractor Standard map Swinging Atwood's machine Tent map Tinkerbell map Van der Pol oscillator Zaslavskii map

Chaos systems	Bouncing ball dynamics Economic bubble Tilt-A-Whirl

Chaos theorists	Michael Berry Leon O. Chua Mitchell Feigenbaum Martin Gutzwiller Brosl Hasslacher Michel Hénon Edward Norton Lorenz Aleksandr Lyapunov Benoît Mandelbrot Henri Poincaré Otto Rössler David Ruelle Oleksandr Mykolaiovych Sharkovsky Floris Takens James A. Yorke

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.