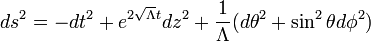Kantowski-Sachs metric

From Wikipedia, the free encyclopedia

In general relativity the Kantowski-Sachs metric describes a homogeneous but anisotropic universe whose spatial section has the topology of 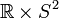{\mathbb {R}}\times S^{{2}}. The metric is:

ds^{{2}}=-dt^{{2}}+e^{{2{\sqrt {\Lambda }}t}}dz^{{2}}+{\frac {1}{\Lambda }}(d\theta ^{{2}}+\sin ^{{2}}\theta d\phi ^{{2}})

The isometry group of this spacetime is 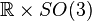{\mathbb {R}}\times SO(3). Remarkably, the isometry group does not act simply transitively on spacetime, nor does it possess a subgroup with simple transitive action.

See also


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.