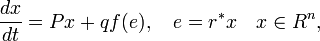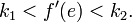Kalman's conjecture

Kalman's conjecture or Kalman problem is a conjecture on absolute stability of nonlinear control system with one scalar nonlinearity, which belongs to the sector of linear stability. Kalman's conjecture is a strengthening of Aizerman's conjecture and is a special case of Markus–Yamabe conjecture. This conjecture was proven false but led to the (valid) sufficient criteria on absolute stability.
Mathematical statement of Kalman's conjecture (Kalman problem)
In 1957 R. E. Kalman in his paper [1] stated the following:
If f(e) in Fig. 1 is replaced by constants K corresponding to all possible values of f'(e), and it is found that the closed-loop system is stable for all such K, then it intuitively clear that the system must be monostable; i.e., all transient solutions will converge to a unique, stable critical point.
Kalman's statement can be reformulated in the following conjecture:[2]
Consider a system with one scalar nonlinearity
where P is a constant n×n matrix, q, r are constant n-dimensional vectors, ∗ is an operation of transposition, f(e) is scalar function, and f(0) = 0. Suppose, f(e) is a differentiable function and the following condition
is valid. Then Kalman's conjecture is that the system is stable in large (i.e. unique stationary point is global attractor) if all linear systems with f(e) = ke, k ∈ (k1, k2) are asymptotically stable.
In Aizerman's conjecture in place of condition on the derivative of nonlinearity it is required that the nonlinearity itself belongs to linear sector.
Kalman's conjecture is true for n ≤ 3 and for n > 3 there are effective methods for construction of counterexamples:[3][4] nonlinearity derivative belongs to the sector of linear stability, and unique stable equilibrium coexists with a stable periodic solution (hidden oscillation).
References
- ↑ Kalman R.E. (1957). "Physical and Mathematical mechanisms of instability in nonlinear automatic control systems". Transactions of ASME 79 (3): 553–566.
- ↑ Leonov G.A., Kuznetsov N.V. (2011). "Algorithms for Searching for Hidden Oscillations in the Aizerman and Kalman Problems". Doklady Mathematics 84 (1): 475–481. doi:10.1134/S1064562411040120.
- ↑ Bragin V.O., Vagaitsev V.I., Kuznetsov N.V., Leonov G.A. (2011). "Algorithms for Finding Hidden Oscillations in Nonlinear Systems. The Aizerman and Kalman Conjectures and Chua's Circuits". Journal of Computer and Systems Sciences International 50 (5): 511–543. doi:10.1134/S106423071104006X.
- ↑ Leonov G.A., Kuznetsov N.V. (2013). "Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits". International Journal of Bifurcation and Chaos 23 (1): art. no. 1330002. doi:10.1142/S0218127413300024.
Further reading
- Leonov G.A., Kuznetsov N.V. (2011). "Analytical-numerical methods for investigation of hidden oscillations in nonlinear control systems". IFAC Proceedings Volumes (IFAC-PapersOnline) 18 (1): 2494–2505. doi:10.3182/20110828-6-IT-1002.03315.