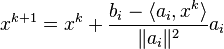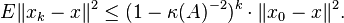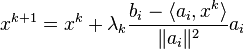Kaczmarz method
The Kaczmarz method or Kaczmarz's algorithm is an iterative algorithm for solving linear systems of equations 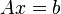 . It was first discovered by the Polish mathematician Stefan Kaczmarz,[1] and was rediscovered in the field of image reconstruction from projections by Richard Gordon, Robert Bender, and Gabor Herman in 1970, where it is called the Algebraic Reconstruction Technique (ART).[2]
. It was first discovered by the Polish mathematician Stefan Kaczmarz,[1] and was rediscovered in the field of image reconstruction from projections by Richard Gordon, Robert Bender, and Gabor Herman in 1970, where it is called the Algebraic Reconstruction Technique (ART).[2]
It is applicable to any linear system of equations, but its computational advantage relative to other methods depends on the system being sparse. It has been demonstrated to be superior, in some biomedical imaging applications, to other methods such as the filtered backprojection method.[3]
It has many applications ranging from computed tomography (CT) to signal processing. It can be obtained also by applying to the hyperplanes, described by the linear system, the method of successive projections onto convex sets (POCS).[4][5]
Algorithm 1: Randomized Kaczmarz algorithm
Let 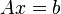 be a linear system and
be a linear system and 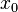 be arbitrary initial approximation to the solution of
be arbitrary initial approximation to the solution of 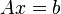 . For
. For  compute:
compute:
where  is chosen from the set
is chosen from the set 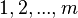 at random, with probability proportional to
at random, with probability proportional to 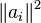 .
.
Under such circumstances 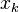 converges exponentially fast to the solution of
converges exponentially fast to the solution of 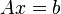 , and the rate of convergence depends only on the scaled condition number
, and the rate of convergence depends only on the scaled condition number  .
.
Theorem
Let  be the solution of
be the solution of 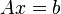 . Then Algorithm 1 converges to
. Then Algorithm 1 converges to  in expectation, with the average error:
in expectation, with the average error:
Proof
There holds
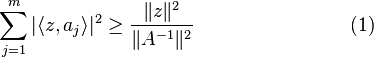 for all
for all 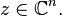
Using the fact that 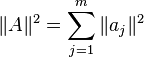 we can write (1) as
we can write (1) as
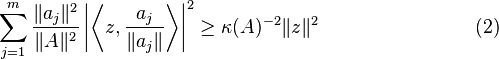 for all
for all 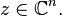
The main point of the proof is to view the left hand side in (2) as an expectation of some random variable. Namely, recall that the solution space of the  equation of
equation of 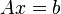 is the hyperplane
is the hyperplane  , whose normal is
, whose normal is  Define a random vector Z whose values are the normals to all the equations of
Define a random vector Z whose values are the normals to all the equations of 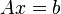 , with probabilities as in our algorithm:
, with probabilities as in our algorithm:
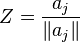 with probability
with probability 
Then (2) says that
 for all
for all 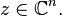
The orthogonal projection  onto the solution space of a random equation of
onto the solution space of a random equation of 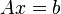 is given by
is given by 
Now we are ready to analyze our algorithm. We want to show that the error  reduces at each step in average (conditioned on the previous steps) by at least the factor of
reduces at each step in average (conditioned on the previous steps) by at least the factor of 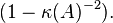 The next approximation
The next approximation  is computed from
is computed from 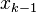 as
as 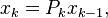 where
where 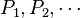 are independent realizations of the random projection
are independent realizations of the random projection 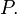 The vector
The vector 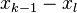 is in the kernel of
is in the kernel of 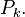 It is orthogonal to the solution space of the equation onto which
It is orthogonal to the solution space of the equation onto which 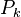 projects, which contains the vector
projects, which contains the vector  (recall that
(recall that  is the solution to all equations). The orthogonality of these two vectors then yields
is the solution to all equations). The orthogonality of these two vectors then yields  To complete the proof, we have to bound
To complete the proof, we have to bound  from below. By the definition of
from below. By the definition of  , we have
, we have 
where  are independent realizations of the random vector
are independent realizations of the random vector 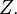
Thus 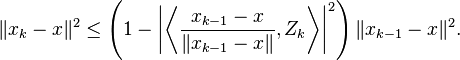
Now we take the expectation of both sides conditional upon the choice of the random vectors 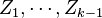 (hence we fix the choice of the random projections
(hence we fix the choice of the random projections  and thus the random vectors
and thus the random vectors 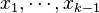 and we average over the random vector
and we average over the random vector  ). Then
). Then
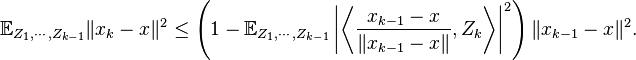
By (3) and the independence,
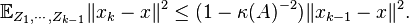
Taking the full expectation of both sides, we conclude that


Algorithm 2: Randomized Kaczmarz algorithm with relaxation
Given a real or complex 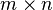 matrix
matrix  and a real or complex vector
and a real or complex vector  , respectively, the Kaczmarz's algorithm iteratively computes an approximation of the solution of the linear systems of equations
, respectively, the Kaczmarz's algorithm iteratively computes an approximation of the solution of the linear systems of equations 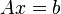 . It does so by converging to the vector
. It does so by converging to the vector 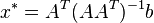 without the need to invert the matrix
without the need to invert the matrix  , which is algorithm's main advantage, especially when the matrix
, which is algorithm's main advantage, especially when the matrix  has a large number of rows.[6] Most generally, algorithm is defined as follows:
has a large number of rows.[6] Most generally, algorithm is defined as follows:
where  ,
,  is the i-th row of the matrix
is the i-th row of the matrix  ,
, 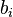 is the i-th component of the vector
is the i-th component of the vector  , and
, and 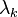 is a relaxation parameter. The above formulae gives a simple iteration routine.
There are various ways for choosing the i-th equation
is a relaxation parameter. The above formulae gives a simple iteration routine.
There are various ways for choosing the i-th equation 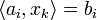 and the relaxation parameter
and the relaxation parameter 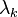 at the k-th iteration.[3]
at the k-th iteration.[3]
If the linear system is consistent, the ART converges to the minimum-norm solution, provided that the iterations start with the zero vector. There are versions of the ART that converge to a regularized weighted least squares solution when applied to a system of inconsistent equations and, at least as far as initial behavior is concerned, at a lesser cost than other iterative methods, such as the conjugate gradient method. [7]
Advances
Recently, a randomized version of the Kaczmarz method for overdetermined linear systems was introduced by Strohmer and Vershynin[8] in which the i-th equation is selected with probability proportional to  .
The superiority of this selection was illustrated with the reconstruction of a bandlimited function from its nonuniformly spaced sampling values. However, it has been pointed out[9] that the reported success by Strohmer and Vershynin depends on the specific choices that were made there in translating the underlying problem, whose geometrical nature is to find a common point of a set of hyperplanes, into a system of algebraic equations. There will always be legitimate algebraic representations of the underlying problem for which the selection method in [8] will perform in an inferior manner.[8][9][10]
.
The superiority of this selection was illustrated with the reconstruction of a bandlimited function from its nonuniformly spaced sampling values. However, it has been pointed out[9] that the reported success by Strohmer and Vershynin depends on the specific choices that were made there in translating the underlying problem, whose geometrical nature is to find a common point of a set of hyperplanes, into a system of algebraic equations. There will always be legitimate algebraic representations of the underlying problem for which the selection method in [8] will perform in an inferior manner.[8][9][10]
Notes
- ↑ Kaczmarz (1937)
- ↑ Gordon, Bender & Herman (1970)
- ↑ 3.0 3.1 Herman (2009)
- ↑ Censor & Zenios (1997)
- ↑ Aster, Borchers & Thurber (2004)
- ↑ Chong & Zak (2008:226)
- ↑ See Herman (2009) and references therein.
- ↑ 8.0 8.1 8.2 Strohmer & Vershynin (2009)
- ↑ 9.0 9.1 Censor, Herman & Jiang (2009)
- ↑ Strohmer & Vershynin (2009b)
References
- Kaczmarz, Stefan (1937), "Angenäherte Auflösung von Systemen linearer Gleichungen" (PDF), Bulletin International de l'Académie Polonaise des Sciences et des Lettres. Classe des Sciences Mathématiques et Naturelles. Série A, Sciences Mathématiques, 35: 355–357
- Chong, Edwin K. P.; Zak, Stanislaw H. (2008), An Introduction to Optimization (3rd ed.), John Wiley & Sons, pp. 226–230
- Gordon, Richard; Bender, Robert; Herman, Gabor (1970), "Algebraic reconstruction techniques (ART) for threedimensional electron microscopy and x-ray photography", Journal of Theoretical Biology 29,: 471–481
- Herman, Gabor (2009), Fundamentals of computerized tomography: Image reconstruction from projection (2nd ed.), Springer
- Censor, Yair; Zenios, S.A. (1997), Parallel optimization: theory, algorithms, and applications, New York: Oxford University Press
- Aster, Richard; Borchers, Brian; Thurber, Clifford (2004), Parameter Estimation and Inverse Problems, Elsevier
- Strohmer, Thomas; Vershynin, Roman (2009), "A randomized Kaczmarz algorithm for linear systems with exponential convergence" (PDF), Journal of Fourier Analysis and Applications 15: 262–278
- Censor, Yair; Herman, Gabor; Jiang, M. (2009), "A note on the behavior of the randomized Kaczmarz algorithm of Strohmer and Vershynin", Journal of Fourier Analysis and Applications 15: 431–436
- Strohmer, Thomas; Vershynin, Roman (2009b), "Comments on the randomized Kaczmarz method", Journal of Fourier Analysis and Applications 15: 437–440
- Vinh Nguyen, Quang; Lumban Gaol, Ford (2011), "Proceedings of the 2011 2nd International Congress on Computer Applications and Computational Science", Springer 2: 465–469
External links
- A randomized Kaczmarz algorithm with exponential convergence
- Comments on the randomized Kaczmarz method
| ||||||||||||||