K-graph C*-algebra
Background
The finitegraph theory in a directed graph form a mathematics category under concatenation called the free object category (which is generated by a graph). The length of a path in  gives a
functor from this category into the natural numbers
gives a
functor from this category into the natural numbers  .
A k-graph is a natural generalistion of this concept which was introduced in[1] by Alex Kumjian and David Pask.
.
A k-graph is a natural generalistion of this concept which was introduced in[1] by Alex Kumjian and David Pask.
Definition
In mathematics, a k-graph (or higher-rank graph, graph of rank k) is a countable category  with domain and codomain maps
with domain and codomain maps  and
and  , together with a functor
, together with a functor 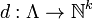 which satisfies the following factorisation property: if
which satisfies the following factorisation property: if 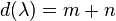 then there are unique
then there are unique  with
with 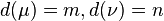 such that
such that 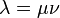 .
.
Examples
- It can be shown that a 1-graph is precisely the path category of a directed graph.
- The category
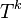 consisting of a single object and k commuting morphisms
consisting of a single object and k commuting morphisms  , together with the map
, together with the map 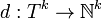 defined
defined  , is a k-graph.
, is a k-graph. - Let
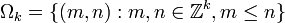 then
then 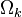 is a k-graph when gifted with the structure maps
is a k-graph when gifted with the structure maps 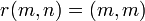 ,
,  ,
, 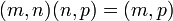 and
and 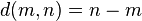 .
.
Notation
The notation for k-graphs is borrowed extensively from the corresponding notation for categories:
- For
 let
let 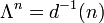 .
. - By the factorisation property it follows that
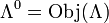 .
. - For
 and
and 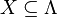 we have
we have 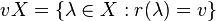 ,
, 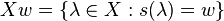 and
and 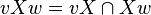 .
. - If
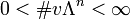 for all
for all  and
and  then
then  is said to be row-finite with no sources.
is said to be row-finite with no sources.
Visualisation - Skeletons
A k-graph is best visualised by drawing its 1-skeleton as a k-coloured graph  where
where
 ,
, 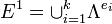 ,
, 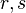 inherited
from
inherited
from  and
and  defined by
defined by 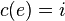 if and only if
if and only if 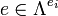 where
where 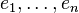 are the canonical
generators for
are the canonical
generators for  . The factorisation property in
. The factorisation property in  for elements
of degree
for elements
of degree 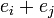 where
where  gives rise to relations between the edges of
gives rise to relations between the edges of
 .
.
C*-algebra
As with graph-algebras one may associate a C*-algebra to a k=graph:
Let  be a row-finite k-graph with no sources then a Cuntz–Kriger
be a row-finite k-graph with no sources then a Cuntz–Kriger  family in a C*-algebra B is a collection
family in a C*-algebra B is a collection 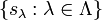 of operators in B such that
of operators in B such that
-
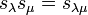 if
if 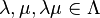 ;
; -
 are mutually orthogonal projections;
are mutually orthogonal projections; - if
 then
then 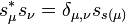 ;
; -
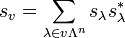 for all
for all  and
and  .
.
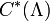 is then the universal C*-algebra generated by a Cuntz–Krieger
is then the universal C*-algebra generated by a Cuntz–Krieger  -family.
-family.
References
- ↑ Kumjian, A.; Pask, D.A. (2000), "Higher rank graph C*-algebras", The New York Journal of Mathematics 6: 1–20
- Raeburn, I., Graph algebras, CBMS Regional Conference Series in Mathematics 103, American Mathematical Society