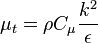K-epsilon turbulence model

From Wikipedia, the free encyclopedia

K-epsilon (k-ε) turbulence model is the most common model used in Computational Fluid Dynamics (CFD) to simulate turbulent conditions. It is a two equation model which gives a general description of turbulence by means of two transport equations (PDEs). The original impetus for the K-epsilon model was to improve the mixing-length model, as well as to find an alternative to algebraically prescribing turbulent length scales in moderate to high complexity flows.^[1] The first transported variable determines the energy in the turbulence and is called turbulent kinetic energy (k). The second transported variable is the turbulent dissipation ( $\epsilon$ ) which determines the rate of dissipation of the turbulent kinetic energy.

Principle

Unlike other turbulence models, k-ε model focuses on the mechanisms that affect the turbulent kinetic energy. The mixing length model lacks this kind of generality.^[2] The underlying assumption of this model is that the turbulent viscosity is isotropic, in other words, the ratio between Reynolds stress and mean rate of deformations is same in all directions.

Standard k-ε turbulence model

The exact k-ε equations contains many unknown and unmeasurable terms. For a much more practical approach, the standard k-ε turbulence model (Launder and Spalding,^[3] 1974) is used which is based on our best understanding of the relevant processes, thus minimizing unknowns and presenting a set of equations which can be applied to a large number of turbulent applications.

For turbulent kinetic energy k

${\frac {\delta (\rho k)}{\delta t}}+{\frac {\delta (\rho ku_{i})}{\delta x_{i}}}={\frac {\delta }{\delta x_{j}}}\left[{\frac {\mu _{t}}{\sigma _{k}}}{\frac {\delta k}{\delta x_{j}}}\right]+2{\mu _{t}}{E_{{ij}}}{E_{{ij}}}-\rho \epsilon$

For dissipation $\epsilon$

${\frac {\delta (\rho \epsilon )}{\delta t}}+{\frac {\delta (\rho \epsilon u_{i})}{\delta x_{i}}}={\frac {\delta }{\delta x_{j}}}\left[{\frac {\mu _{t}}{\sigma _{\epsilon }}}{\frac {\delta \epsilon }{\delta x_{j}}}\right]+C_{{1\epsilon }}{\frac {\epsilon }{k}}2{\mu _{t}}{E_{{ij}}}{E_{{ij}}}-C_{{2\epsilon }}\rho {\frac {\epsilon ^{2}}{k}}$

In other words,

Rate of change of k or ε + Transport of k or ε by convection = Transport of k or ε by diffusion + Rate of production of k or ε - Rate of destruction of k or ε

where

$u_{i}$ represents velocity component in corresponding direction

$E_{{ij}}$ represents component of rate of deformation

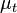$\mu _{t}$ represents eddy viscosity

$\mu _{t}=\rho C_{{\mu }}{\frac {k^{2}}{\epsilon }}$

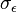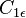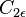The equations also consist of some adjustable constants $\sigma _{k}$ , $\sigma _{{\epsilon }}$ , $C_{{1\epsilon }}$ and $C_{{2\epsilon }}$ . The values of these constants have been arrived at by numerous iterations of data fitting for a wide range of turbulent flows. These are as follows:^[2]

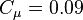
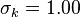
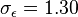
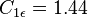
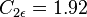
$C_{{\mu }}=0.09$ $\sigma _{k}=1.00$ $\sigma _{{\epsilon }}=1.30$ $C_{{1\epsilon }}=1.44$ $C_{{2\epsilon }}=1.92$

Applications

The k-ε model has been tailored specifically for planar shear layers and recirculating flows. This model is the most widely used and validated turbulence model with applications ranging from industrial to environmental flows, which explains its popularity. It is usually useful for free-shear layer flows with relatively small pressure gradients as well as in confined flows where the Reynolds shear stresses are most important.^[4] It can also be stated as the simplest turbulence model for which only initial and/or boundary conditions needs to be supplied.
However it is more expensive in terms of memory than the mixing length model as it requires two extra PDEs. This model would be an inappropriate choice for problems such as inlets and compressors as accuracy has been shown experimentally to be reduced for flows containing large adverse pressure gradients. The k-ε model also performs poorly in a variety of important cases such as unconfined flows,^[5] curved boundary layers, rotating flows and flows in non-circular ducts.

Other models

Following are some more models which are usually employed.

Realisable k-epsilon model
Reynolds stress equation model
Re-Normalisation Group (RNG) k-epsilon model

References

↑ K-epsilon models
↑ 2.0 2.1 Henk Kaarle Versteeg, Weeratunge Malalasekera (2007). An Introduction to Computational Fluid Dynamics: The Finite Volume Method. Pearson Education Limited. ISBN 9780131274983.
↑ The numerical computation of turbulent flows
↑ The Turbulence Model Can Make a Big Difference in Your Results
↑ P Bradshaw (1987), Turbulent Secondary Flows, Annual Review of Fluid Mechanics, doi:10.1146/annurev.fl.19.010187.000413?journalCode=fluid

Notes

'An Introduction to Computational Fluid Dynamics: The Finite Volume Method (2nd Edition)' , H. Versteeg, W. Malalasekera; Pearson Education Limited; 2007; ISBN 0131274988
'Turbulence Modeling for CFD' 2nd Ed. , Wilcox C. D. ; DCW Industries ; 1998 ; ISBN 0963605100
'An introduction to turbulence and its measurement' , Bradshaw, P. ; Pergamon Press ; 1971 ; ISBN 0080166210

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.