Küpfmüller's uncertainty principle

From Wikipedia, the free encyclopedia

Küpfmüller's uncertainty principle states that the relation of the rise time of a bandlimited signal to its bandwidth is a constant.

$\Delta f\Delta t\geq k$

with $k$ either $1$ or ${\frac {1}{2}}$

Proof

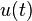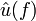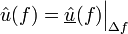A bandlimited signal $u(t)$ with fourier transform ${\hat {u}}(f)$ in frequency space is given by the multiplication of any signal $\underline {{\hat {u}}}(f)$ with ${\hat {u}}(f)={{\underline {{\hat {u}}}(f)}}{{{\Big |}}_{{\Delta f}}}$ with a rectangular function of width $\Delta f$

${\hat {g}}(f)=\operatorname {rect}\left({\frac {f}{\Delta f}}\right)=\chi _{{[-\Delta f/2,\Delta f/2]}}(f):={\begin{cases}1&|f|\leq \Delta f/2\\0&{\text{else}}\end{cases}}$

as (applying the convolution theorem)

${\hat {g}}(f)\cdot {\hat {u}}(f)=(g*u)(t)$

Since the fourier transform of a rectangular function is a sinc function and vice versa, follows

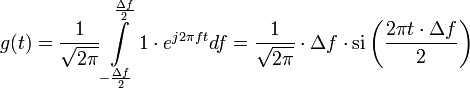
$g(t)={\frac 1{{\sqrt {2\pi }}}}\int \limits _{{-{\frac {\Delta f}{2}}}}^{{{\frac {\Delta f}{2}}}}1\cdot e^{{j2\pi ft}}df={\frac 1{{\sqrt {2\pi }}}}\cdot \Delta f\cdot \operatorname {si}\left({\frac {2\pi t\cdot \Delta f}{2}}\right)$

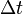Now the first root of $g(t)$ is at $\pm {\frac {1}{\Delta f}}$ , which is the rise time $\Delta t$ of the pulse $g(t)$ , now follows

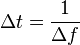
$\Delta t={\frac {1}{\Delta f}}$

Equality is given as long as 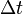$\Delta t$ is finite.

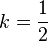Regarding that a real signal has both positive and negative frequencies of the same frequency band, $\Delta f$ becomes $2\cdot \Delta f$ , which leads to $k={\frac {1}{2}}$ instead of $k=1$

References

Küpfmüller, Karl; Kohn, Gerhard (2000), Theoretische Elektrotechnik und Elektronik, Berlin, Heidelberg: Springer-Verlag, ISBN 978-3-540-56500-0 .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.