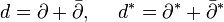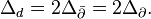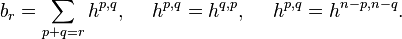Kähler manifold

From Wikipedia, the free encyclopedia

In mathematics and especially differential geometry, a Kähler manifold is a manifold with three mutually compatible structures; a complex structure, a Riemannian structure, and a symplectic structure.

Kähler manifolds find important applications in the field of algebraic geometry where they represent generalizations of complex projective algebraic varieties via the Kodaira embedding theorem (Hartshorne 1977). They are named after German mathematician Erich Kähler.

Definitions

Since Kähler manifolds are naturally equipped with several compatible structures, there are many equivalent ways of creating Kähler forms.

Symplectic viewpoint

A Kähler manifold is a symplectic manifold $(K,\omega )$ equipped with an integrable almost-complex structure which is compatible with the symplectic form.^[1]

Complex viewpoint

A Kähler manifold is a Hermitian manifold whose associated Hermitian form is closed. The closed Hermitian form is called the Kähler metric.

Equivalence of definitions

Every Hermitian manifold $K$ is a complex manifold which comes naturally equipped with a Hermitian form $h$ and an integrable, almost complex structure $J$ . Assuming that $h$ is closed, there is a canonical symplectic form defined as $\omega ={\frac i2}(h-{\bar h})$ which is compatible with $J$ , hence satisfying the first definition.

On the other hand, any symplectic form compatible with an almost complex structure must be a complex differential form of type $(1,1)$ , written in a coordinate chart $(U,z_{i})$ as

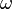$\omega ={\frac i2}\sum _{{j,k}}h_{{jk}}dz_{j}\wedge d{\bar {z_{k}}}$

for $h_{{jk}}\in C^{\infty }(U,{\mathbb C})$ . The added assertions that $\omega$ be real-valued, closed, and non-degenerate guarantee that the $h_{{jk}}$ define Hermitian forms at each point in $K$ .^[1]

Connection between Hermitian and symplectic definitions

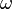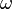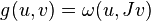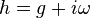Let $h$ be the Hermitian form, $\omega$ the symplectic form, and $J$ the almost complex structure. Since $\omega$ and $J$ are compatible, the new form $g(u,v)=\omega (u,Jv)$ is Riemannian.^[1] One may then summarize the connection between these structures via the identity $h=g+i\omega$ .

Kähler potentials

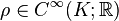If $K$ is a complex manifold, it can be shown^[1] that every strictly plurisubharmonic function $\rho \in C^{\infty }(K;{\mathbb R})$ gives rise to a Kähler form as

$\omega ={\frac i2}\partial {\bar \partial }\rho$

where $\partial ,{\bar \partial }$ are the Dolbeault operators. The function $\rho$ is said to be a Kähler potential.

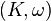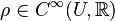In fact, utilizing the holomorphic version of the Poincaré lemma, a partial converse holds true locally. More specifically, if $(K,\omega )$ is a Kähler manifold then about every point $p\in K$ there is a neighbourhood $U$ containing $p$ and a function $\rho \in C^{\infty }(U,{\mathbb R})$ such that $\omega \vert _{U}=i\partial {\bar \partial }\rho$ and here $\rho$ is termed a (local) Kähler potential.

Ricci tensor and Kähler manifolds

see Kähler manifolds in Ricci tensor.

The Laplacians on Kähler manifolds

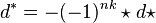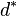Let $\star$ be the Hodge operator and then on an differential manifold X we can define the Laplacian as $\Delta _{d}=dd^{*}+d^{*}d$ where $d$ is the exterior derivative and $d^{*}=-(-1)^{{nk}}\star d\star$ . Furthermore if X is Kähler then $d$ and $d^{*}$ are decomposed as

$d=\partial +{\bar {\partial }},\ \ \ \ d^{*}=\partial ^{*}+{\bar {\partial }}^{*}$

and we can define another Laplacians

$\Delta _{{{\bar {\partial }}}}={\bar {\partial }}{\bar {\partial }}^{*}+{\bar {\partial }}^{*}{\bar {\partial }},\ \ \ \ \Delta _{\partial }=\partial \partial ^{*}+\partial ^{*}\partial$

that satisfy

$\Delta _{d}=2\Delta _{{{\bar {\partial }}}}=2\Delta _{\partial }.$

From these facts we obtain the Hodge decomposition (see Hodge theory)

${\mathbf {H^{r}}}=\bigoplus _{{p+q=r}}{\mathbf {H}}^{{p,q}}$

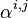where ${\mathbf {H^{r}}}$ is r-degree harmonic form and ${\mathbf {H}}^{{p,q}}$ is {p,q}-degree harmonic form on X. Namely, an differential form $\alpha$ is harmonic if and only if each $\alpha ^{{i,j}}$ belong to the {i,j}-degree harmonic form.

Further, if X is compact then we obtain

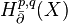$H^{p}(X,\Omega ^{q})\simeq H_{{{\bar {\partial }}}}^{{p,q}}(X)\simeq {\mathbf {H}}^{{p,q}}$

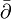where $H_{{{\bar {\partial }}}}^{{p,q}}(X)$ is ${\bar {\partial }}$ -harmonic cohomology group. This means that if $\alpha$ is an differential form with {p,q}-degree there is only one element in {p,q}-harmonic form due to Dolbeault theorem.

Let 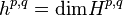$h^{{p,q}}={\text{dim}}H^{{p,q}}$ , called Hodge number, then we obtain

$b_{r}=\sum _{{p+q=r}}h^{{p,q}},\ \ \ \ h^{{p,q}}=h^{{q,p}},\ \ \ \ h^{{p,q}}=h^{{n-p,n-q}}.$

The LHS of the first identity, b_r, is r-th Betti number, the second identity comes from that since the Laplacian 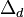$\Delta _{d}$ is a real operator $H^{{p,q}}=\overline {H^{{q,p}}}$ and the third identity comes from Serre duality.

Applications

On a Kähler manifold, the associated Kähler form and metric are called Kähler–Einstein (or sometimes Einstein–Kähler) if its Ricci tensor is proportional to the metric tensor, 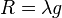$R=\lambda g$ , for some constant λ. This name is a reminder of Einstein's considerations about the cosmological constant. See the article on Einstein manifolds for more details.

Originally the Kähler condition is independent on the Einstein condition, in which Ricci tensor is proportional to Riemannian metric with constant real number. The important point is that if X is Kähler then Christoffel symbols 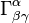$\Gamma _{{\beta \gamma }}^{\alpha }$ vanish and Ricci curvature is much simplified. The Kähler condition, therefore, is closely related with Ricci curvature. In fact Aubin and Yau prove the Calabi conjecture using the fact that on a compact Kähler manifold with the first Chern class c₁=0 there is a unique Ricci-flat Kähler metric in each Kähler class. But in non-compact case the situation turns to be more complicated and the final solution might not be reached.

Examples

Complex Euclidean space Cⁿ with the standard Hermitian metric is a Kähler manifold.
A torus Cⁿ/Λ (Λ a full lattice) inherits a flat metric from the Euclidean metric on Cⁿ, and is therefore a compact Kähler manifold.
Every Riemannian metric on a Riemann surface is Kähler, since the condition for ω to be closed is trivial in 2 (real) dimensions.
Complex projective space CPⁿ admits a homogeneous Kähler metric, the Fubini–Study metric. An Hermitian form in (the vector space) C^n + 1 defines a unitary subgroup U(n + 1) in GL(n + 1,C); a Fubini–Study metric is determined up to homothety (overall scaling) by invariance under such a U(n + 1) action. By elementary linear algebra, any two Fubini–Study metrics are isometric under a projective automorphism of CPⁿ, so it is common to speak of "the" Fubini–Study metric.
The induced metric on a complex submanifold of a Kähler manifold is Kähler. In particular, any Stein manifold (embedded in Cⁿ) or projective algebraic variety (embedded in CPⁿ) is of Kähler type. This is fundamental to their analytic theory.
The unit complex ball Bⁿ admits a Kähler metric called the Bergman metric which has constant holomorphic sectional curvature.
Every K3 surface is Kähler (by a theorem of Y.-T. Siu).

An important subclass of Kähler manifolds are Calabi–Yau manifolds.

Properties

(Deligne et al. 1975) showed that all Massey products vanish on a Kähler manifold. Manifolds with such vanishing are formal: their real homotopy type follows ("formally") from their real cohomology ring.

References

↑ 1.0 1.1 1.2 1.3 Canas da Silva, Ana (2008). Lectures on Symplectic Geometry. Springer. ISBN 978-3540421955.

Deligne, P.; Griffiths, Ph.; Morgan, J.; Sullivan, D., (1975), "Real homotopy theory of Kähler manifolds", Invent. Math. 29: 245–274, doi:10.1007/BF01389853
Hartshorne, Robin (1977), Algebraic Geometry, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90244-9, OCLC 13348052, MR 0463157
Alan Huckleberry and Tilman Wurzbacher, eds. Infinite Dimensional Kähler Manifolds (2001), Birkhauser Verlag, Basel ISBN 3-7643-6602-8.
Andrei Moroianu, Lectures on Kähler Geometry (2007), London Mathematical Society Student Texts 69, Cambridge ISBN 978-0-521-68897-0.
Andrei Moroianu, Lectures on Kähler Geometry (2004), http://www.math.polytechnique.fr/~moroianu/tex/kg.pdf
André Weil, Introduction à l'étude des variétés kählériennes (1958)

External links

Hazewinkel, Michiel, ed. (2001), "Kähler manifold", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.