Josephson penetration depth

From Wikipedia, the free encyclopedia

In superconductivity, Josephson penetration depth characterizes the typical length on which an externally-applied magnetic field penetrates into the long Josephson junction. Josephson penetration depth is usually denoted as $\lambda _{J}$ and is given by the following expression (in SI):

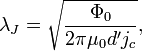
$\lambda _{J}={\sqrt {{\frac {\Phi _{0}}{2\pi \mu _{0}d'j_{c}}}}},$

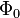where $\Phi _{0}$ is the magnetic flux quantum, 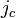$j_{c}$ is the critical current density 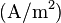${\mathrm {(A/m^{2})}}$ , and $d'$ characterizes the inductance of the superconducting electrodes

$d'=d_{I}+\lambda _{1}\coth \left({\frac {d_{1}}{\lambda _{1}}}\right)+\lambda _{2}\coth \left({\frac {d_{2}}{\lambda _{2}}}\right),$

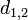where $d_{I}$ is the thickness of the Josephson barrier (usually insulator), $d_{{1,2}}$ are the thicknesses of superconducting electrodes, and 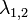$\lambda _{{1,2}}$ are their London penetration depths.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.