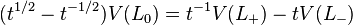Jones polynomial
In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984.[1] Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable 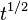 with integer coefficients.[2]
with integer coefficients.[2]
Definition by the bracket
Suppose we have an oriented link 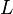 , given as a knot diagram. We will define the Jones polynomial,
, given as a knot diagram. We will define the Jones polynomial, 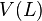 , using Kauffman's bracket polynomial, which we denote by
, using Kauffman's bracket polynomial, which we denote by  . Note that here the bracket polynomial is a Laurent polynomial in the variable
. Note that here the bracket polynomial is a Laurent polynomial in the variable  with integer coefficients.
with integer coefficients.
First, we define the auxiliary polynomial (also known as the normalized bracket polynomial)
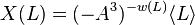 ,
,
where  denotes the writhe of
denotes the writhe of 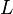 in its given diagram. The writhe of a diagram is the number of positive crossings (
in its given diagram. The writhe of a diagram is the number of positive crossings (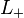 in the figure below) minus the number of negative crossings (
in the figure below) minus the number of negative crossings (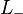 ). The writhe is not a knot invariant.
). The writhe is not a knot invariant.
 is a knot invariant since it is invariant under changes of the diagram of
is a knot invariant since it is invariant under changes of the diagram of 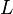 by the three Reidemeister moves. Invariance under type II and III Reidemeister moves follows from invariance of the bracket under those moves. The bracket polynomial is known to change by multiplication by
by the three Reidemeister moves. Invariance under type II and III Reidemeister moves follows from invariance of the bracket under those moves. The bracket polynomial is known to change by multiplication by  under a type I Reidemeister move. The definition of the
under a type I Reidemeister move. The definition of the  polynomial given above is designed to nullify this change, since the writhe changes appropriately by +1 or -1 under type I moves.
polynomial given above is designed to nullify this change, since the writhe changes appropriately by +1 or -1 under type I moves.
Now make the substitution  in
in  to get the Jones polynomial
to get the Jones polynomial 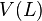 . This results in a Laurent polynomial with integer coefficients in the variable
. This results in a Laurent polynomial with integer coefficients in the variable 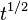 .
.
Definition by braid representation
Jones' original formulation of his polynomial came from his study of operator algebras. In Jones' approach, it resulted from a kind of "trace" of a particular braid representation into an algebra which originally arose while studying certain models, e.g. the Potts model, in statistical mechanics.
Let a link L be given. A theorem of Alexander's states that it is the trace closure of a braid, say with n strands. Now define a representation  of the braid group on n strands, Bn, into the Temperley–Lieb algebra TLn with coefficients in
of the braid group on n strands, Bn, into the Temperley–Lieb algebra TLn with coefficients in ![{\mathbb Z}[A,A^{{-1}}]](/2014-wikipedia_en_all_02_2014/I/media/4/0/c/5/40c589bb3f3bba252ca2fa2c5ae69c4b.png) and
and 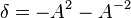 . The standard braid generator
. The standard braid generator  is sent to
is sent to  , where
, where  are the standard generators of the Temperley–Lieb algebra. It can be checked easily that this defines a representation.
are the standard generators of the Temperley–Lieb algebra. It can be checked easily that this defines a representation.
Take the braid word 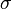 obtained previously from L and compute
obtained previously from L and compute 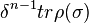 where tr is the Markov trace. This gives
where tr is the Markov trace. This gives  , where
, where 
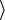 is the bracket polynomial. This can be seen by considering, as Kauffman did, the Temperley–Lieb algebra as a particular diagram algebra.
is the bracket polynomial. This can be seen by considering, as Kauffman did, the Temperley–Lieb algebra as a particular diagram algebra.
An advantage of this approach is that one can pick similar representations into other algebras, such as the R-matrix representations, leading to "generalized Jones invariants".
Properties
The Jones polynomial is characterized by the fact that it takes the value 1 on any diagram of the unknot and satisfies the following skein relation:
where 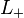 ,
, 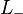 , and
, and 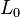 are three oriented link diagrams that are identical except in one small region where they differ by the crossing changes or smoothing shown in the figure below:
are three oriented link diagrams that are identical except in one small region where they differ by the crossing changes or smoothing shown in the figure below:
.svg.png)
The definition of the Jones polynomial by the bracket makes it simple to show that for a knot  , the Jones polynomial of its mirror image is given by substitution of
, the Jones polynomial of its mirror image is given by substitution of 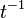 for
for  in
in 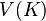 . Thus, an amphichiral knot, a knot equivalent to its mirror image, has palindromic entries in its Jones polynomial. See the article on skein relation for an example of a computation using these relations.
. Thus, an amphichiral knot, a knot equivalent to its mirror image, has palindromic entries in its Jones polynomial. See the article on skein relation for an example of a computation using these relations.
Link with Chern–Simons theory
As first shown by Edward Witten, the Jones polynomial of a given knot  can be obtained by considering Chern–Simons theory on the three-sphere with gauge group SU(2), and computing the vacuum expectation value of a Wilson loop
can be obtained by considering Chern–Simons theory on the three-sphere with gauge group SU(2), and computing the vacuum expectation value of a Wilson loop 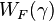 , associated to
, associated to  , and the fundamental representation
, and the fundamental representation  of
of 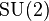 .
.
Open problems
- Is there a nontrivial knot with Jones polynomial equal to that of the unknot? It is known that there are nontrivial links with Jones polynomial equal to that of the corresponding unlinks by the work of Morwen Thistlethwaite.
See also
Notes
References
- Vaughan Jones, The Jones Polynomial
- Colin Adams, The Knot Book, American Mathematical Society, ISBN 0-8050-7380-9
- H. Kauffman, Louis (1987). "State models and the jones polynomial". Topology 26 (3): 395–407. doi:10.1016/0040-9383(87)90009-7. Retrieved 22 December 2012. (explains the definition by bracket polynomial and its relation to Jones' formulation by braid representation)
- Lickorish, W. B. Raymond (1997). An introduction to knot theory. New York; Berlin; Heidelberg; Barcelona; Budapest; Hong Kong; London; Milan; Paris; Santa Clara; Singapore; Tokyo: Springer. p. 175. ISBN 978-0-387-98254-0.
- THISTLETHWAITE, MORWEN (2001). "LINKS WITH TRIVIAL JONES POLYNOMIAL". Journal of Knot Theory and Its Ramifications 10 (04): 641–643. doi:10.1142/S0218216501001050.
- Eliahou, Shalom; Kauffman, Louis H.; Thistlethwaite, Morwen B. (2003). "Infinite families of links with trivial Jones polynomial". Topology 42 (1): 155–169. doi:10.1016/S0040-9383(02)00012-5.
External links
- Hazewinkel, Michiel, ed. (2001), "Jones-Conway polynomial", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Links with trivial Jones polynomial by Morwen Thistlethwaite
| |||||||||||||||||||||||